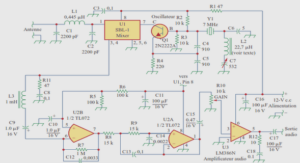
Wave propagation

Waves, as summarized in the insightful review by Keller (1979), are disturbances that propagate through space and time, usually by transference of energy. Propagation is the process of travel or movement from one place to another. Thus wave propagation is another name for the movement of a physical disturbance, often in an oscillatory manner. The example which has been recognized longest is that of the motion of waves on the surface of water. Another is sound, which was known to be a wave motion at least by the time of the magnificent English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian Sir Isaac Newton (1643–1727). In 1690 the Dutch mathematician, astronomer, and physicist Christiaan Huygens (1629–1695) proposed that light is also a wave motion. Gradually other types of waves were recognized. By the end of the nineteenth century elastic waves of various kinds were known, electromagnetic waves had been produced, etc. In the twentieth century matter waves governed by quantum mechanics were discovered, and an active search is still underway for gravitational waves. A discussion on the origin and development of the modern concept of wave is given by Manacorda (1991). The laws of physics provide systems of one or more partial differential equations governing each type of wave. Any particular case of wave propagation is governed by the appropriate equations, together with certain auxiliary conditions. These may include initial conditions, boundary conditions, radiation conditions, asymptotic decaying conditions, regularity conditions, etc. The differential equations together with the auxiliary conditions constitute a mathematical problem for the determination of the wave motion. These problems are the subject matter of the mathematical theory of wave propagation. Some references on this subject that we can mention are Courant & Hilbert (1966), Elmore & Heald (1969), Felsen & Marcuwitz (2003), and Morse & Feshbach (1953). Maxwell’s equations of electromagnetic theory and Schrodinger’s equation in quantum ¨ mechanics are both usually linear. They are named after the Scottish mathematician and theoretical physicist James Clerk Maxwell (1831–1879) and the Austrian physicist Erwin Rudolf Josef Alexander Schrodinger (1887–1961). Furthermore, the equations governing ¨ most waves can be linearized to describe small amplitude waves. Examples of these linearized equations are the scalar wave equation of acoustics and its time-harmonic version, the Helmholtz equation, which receives its name from the German physician and physicist Hermann Ludwig Ferdinand von Helmholtz (1821–1894). Another example is the Laplace equation in hydrodynamics, in which case it is the boundary condition which is linearized and not the equation itself. This equation is named after the French mathematician and astronomer Pierre Simon, marquis de Laplace (1749–1827). Such linear equations with linear auxiliary conditions are the subject of the theory of linear wave propagation. It is this theory which we shall consider. The classical researchers were concerned with obtaining exact and explicit expressions for the solutions of wave propagation problems. Because the problems were linear, they constructed these expressions by superposition, i.e., by linear combination, of particular solutions. The particular solutions had to be simple enough to be found explicitly and the problem had to be special enough for the coefficients in the linear combination to be found. One of the devised methods is the image method (cf., e.g., Morse & Feshbach 1953), in which the particular solution is that due to a point source in the whole space. The domains to which the method applies must be bounded by one or several planes on which the field or its normal derivative vanishes. In some cases it is possible to obtain the solution due to a point source in such a domain by superposing the whole space solution due to the source and the whole space solutions due to the images of the source in the bounding planes. Unfortunately the scope of this method is very limited, but when it works it yields a great deal of insight into the solution and a simple expression for it. The image method also applies to the impedance boundary condition, in which a linear combination of the wave function and its normal derivative vanishes on a bounding plane. Then the image of a point source is a point source plus a line of sources with exponentially increasing or decreasing strengths. The line extends from the image point to infinity in a direction normal to the plane. These results can be also extended for impedance boundary conditions with an oblique derivative instead of a normal derivative (cf. Gilbarg & Trudinger 1983, Keller 1981), in which case the line of images is parallel to the direction of differentiation. The major classical method is nonetheless that of separation of variables (cf., e.g., Evans 1998, Weinberger 1995). In this method the particular solutions are products of functions of one variable each, and the desired solution is a series or integral of these product solutions, with suitable coefficients. It follows from the partial differential equation that the functions of one variable each satisfy certain ordinary differential equations. Most of the special functions of classical analysis arose in this way, such as those of Bessel, Neumann, Hankel, Mathieu, Struve, Anger, Weber, Legendre, Hermite, Laguerre, Lame,´ Lommel, etc. To determine the coefficients in the superposition of the product solutions, the method of expanding a function as a series or integral of orthogonal functions was developed. In this way the theory of Fourier series originated, and also the method of integral transforms, including those of Fourier, Laplace, Hankel, Mellin, Gauss, etc. Despite its much broader scope than the image method, the method of separation of variables is also quite limited. Only very special partial differential equations possess enough product solutions to be useful. For example, there are only 13 coordinate systems in which the three-dimensional Laplace equation has an adequate number of such solutions, and there are only 11 coordinate systems in which the three-dimensional Helmholtz equation does. Furthermore only for very special boundaries can the expansion coefficients  be found by the use of orthogonal functions. Generally they must be complete coordinate surfaces of a coordinate system in which the equation is separable. Another classical method is the one of eigenfunction expansions (cf. Morse & Feshbach 1953, Butkov 1968). In this case the solutions are expressed as sums or integrals of eigenfunctions, which are themselves solutions of partial differential equations. This method was developed by Lord Rayleigh and others as a consequence of partial separation of variables. They sought particular solutions which were products of a function of one variable (e.g., time) multiplied by a function of several variables (e.g., spatial coordinates). This method led to the use of eigenfunction expansions, to the introduction of adjoint problems, and to other aspects of the theory of linear operators. It also led to the use of variational principles for estimating eigenvalues and approximating eigenfunctions, such as the Rayleigh-Ritz method. These procedures are needed because there exists no way for finding eigenvalues and eigenfunctions explicitly in general. However, if the eigenfunction problem is itself separable, it can be solved by the method of separation of variables. Finally, there is the method of converting a problem into an integral equation with the aid of a Green’s function (cf., e.g., Courant & Hilbert 1966). But generally the integral equation cannot be solved explicitly. In some cases it can be solved by means of integral transforms, but then the original problem can also be solved in this way. In more recent times several other methods have also been developed, which use, e.g., asymptotic analysis, special transforms, among other theoretical tools. A brief account on them can be found in Keller (1979). 

Numerical methods

All the previously mentioned methods to solve wave propagation problems are analytic and they require that the involved domains have some rather specific geometries to be used satisfactorily. In the method of variable separation, e.g., the domain should be described easily in the chosen coordinate system so as to be used effectively. The advent of modern computers and their huge calculation power made it possible to develop a whole new range of methods, the so-called numerical methods. These methods are not concerned with finding an exact solution to the problem, but rather with obtaining an approximate solution that stays close enough to the exact one. The basic idea in any numerical method for differential equations is to discretize the given continuous problem with infinitely many degrees of freedom to obtain a discrete problem or system of equations with only finitely many unknowns that may be solved using a computer. At the end of the discretization procedure, a linear matrix system is obtained, which is what finally is programmed into the computer. a) Bounded domains Two classes of numerical methods are mainly used to solve boundary-value problems on bounded domains: the finite difference method (FDM) and the finite element method (FEM). Both yield sparse and banded linear matrix systems. In the FDM, the discrete problem is obtained by replacing the derivatives with difference quotients involving the values of the unknown at certain (finitely many) points, which conform the discret mesh and which are placed typically at the intersections of mutually perpendicular lines. The FDM is easy to implement, but it becomes very difficult to adapt it to more complicated geometries of the domain. A reference for the FDM is Rappaz & Picasso (1998). The FEM, on the other hand, uses a Galerkin scheme on the variational or weak formulation of the problem. Such a scheme discretizes a boundary-value problem from its weak formulation by approximating the function space of the solution through a finite set of basis functions, and receives its name from the Russian mathematician and engineer Boris Grigoryevich Galerkin (1871–1945). The FEM is thus based on the discretization of the solution’s function space rather than of the differential operator, as is the case with the FDM. The FEM is not so easy to implement as the FDM, since finite element interaction integrals have to be computed to build the linear matrix system. Nevertheless, the FEM is very flexible to be adapted to any reasonable geometry of the domain by choosing adequately the involved finite elements. It was originally introduced by engineers in the late 1950’s as a method to solve numerically partial differential equations in structural engineering, but since then it was further developed into a general method for the numerical solution of all kinds of partial differential equations, having thus applications in many areas of science and engineering. Some references for this method are Ciarlet (1979), Gockenbach (2006), and Johnson (1987). Meanwhile, several other classes of numerical methods for the treatment of differential equations have arisen, which are related to the ones above. Among them we can mention the collocation method (CM), the spectral method (SM), and the finite volume method (FVM). In the CM an approximation is sought in a finite element space by requiring the differential equation to be satisfied exactly at a finite number of collocation points, rather than by an orthogonality condition. The SM, on the other hand, uses globally defined functions, such as eigenfunctions, rather than piecewise polynomials approximating functions, and the discrete solution may be determined by either orthogonality or collocation. The FVM applies to differential equations in divergence form. This method is based on approximating the boundary integral that results from integrating over an arbitrary volume and transforming the integral of the divergence into an integral of a flux over the boundary. All these methods deal essentially with bounded domains, since infinite unbounded domains cannot be stored into a computer with a finite amount of memory. For further details on these methods we refer to Sloan et al. (2001). 

Unbounded domains 

In the case of wave propagation problems, and in particular of scattering problems, the involved domains are usually unbounded. To deal with this situation, two different approaches have been devised: domain truncation and integral equation techniques. Both approaches result in some sort of bounded domains, which can then be discretized numerically without problems. In the first approach, i.e., the truncation of the domain, some sort of boundary condition has to be imposed on the truncated (artificial) boundary. Techniques that operate in this way are the Dirichlet-to-Neumann (DtN) or Steklov-Poincare operator, artificial boundaryonditions (ABC), perfectly matched layers (PML), and the infinite element method (IEM). The DtN operator relates on the truncated boundary curve the Dirichlet and the Neumann data, i.e., the value of the solution and of its normal derivative. Thus, the knowledge of the problem’s solution outside the truncated domain, either by a series or an integral representation, allows its use as a boundary condition for the problem inside the truncated domain. Explicit expressions for the DtN operator are usually quite difficult to obtain, except for some few specific geometries. We refer to Givoli (1999) for further details on this operator. In the case of an ABC, a condition is imposed on the truncated boundary that allows the passage only of outgoing waves and eliminates the ingoing ones. The ABC has the disadvantage that it is a global boundary condition, i.e., it specifies a coupling of the values of the solution on the whole artificial boundary by some integral expression. The same holds for the DtN operator, which can be regarded as some sort of ABC. There exist in general only approximations for an ABC, which work well when the wave incidence is nearly normal, but not so well when it is very oblique. Some references for ABC are Nataf (2006) and Tsynkov (1998). In the case of PML, an absorbing layer of finite depth is placed around the truncated boundary so as to absorb the outgoing waves and reduce as much as possible their reflections back into the truncated domain’s interior. On the absorbing layer, the problem is stated using a dissipative wave equation. For further details on PML we refer to Johnson (2008). The IEM, on the other hand, avoids the need of an artificial boundary by partitioning the complement of the truncated domain into a finite amount of so-called infinite elements. These infinite elements reduce to finite elements on the coupling surface and are described in some appropriate coordinate system. References for the IEM and likewise for the other techniques are Ihlenburg (1998) and Marburg & Nolte (2008). Interesting reviews of several of these methods can be also found in Thompson (2005) and Zienkiewicz & Taylor (2000). On the whole, once the domain is truncated with any one of the mentioned techniques, the problem can be solved numerically by using the FEM, the FDM, or some other numerical method that works well with bounded domains. This approach has nonetheless the drawback that the discretization of the additional truncated boundary may produce undesired reflections of the outgoing waves back towards the interior of the truncated domain, due the involved numerical approximations. It is in fact the second approach, i.e., the integral equation techniques, the one that is of our concern throughout this thesis. This approach takes advantage of the fact that the wave propagation problem can be converted into an integral equation with the help of a Green’s function. The integral equation is built in such a way that its support lies on a bounded region, e.g., the domain’s boundary. Even though we mentioned that this approach may not be so practical to find an analytic solution, it becomes very useful when it is combined with an appropriate numerical method to solve the integral equation. Typically either a collocation method or a finite element method is used for this purpose. The latter is based on a variational formulation and is thus numerically more stable and accurate than the former, particularly when the involved geometries contain corners or are otherwise complicated. At the end, the general solution of the problem is retrieved by means of an integral representation formula that requires the solution of the previously solved integral equation. Of course, integral equation techniques can be likewise used to solve wave propagation 6 problems in bounded domains. A big advantage of these techniques is their simplicity to represent the far field of the solution. Some references on integral equation techniques are the books of Hsiao & Wendland (2008), Ned´ elec (2001), and Steinbach (2008). ´ The drawback of integral equation techniques is their more complex mathematical treatment and the requirement of knowing the Green’s function of the system. It is the Green’s function that stores the information of the system’s physics throughout the considered domain and which allows to collapse the problem towards an integral equation. The Green’s function is usually problematic to integrate, since it corresponds to the solution of the homogeneous system subject to a singularity load, e.g., the electrical field arising from a point charge. Integrating such singular fields is not easy in general. For simple element geometries, like straight segments or planar triangles, analytical integration can be used. For more general elements it is possible to design purely numerical schemes that adapt to the singularity, but at a great computational cost. When the source point and target element where the integration is done are far apart, then the integration becomes easier due to the smooth asymptotic decay of the Green’s function. It is this feature that is typically employed in schemes designed to accelerate the involved computations, e.g., in fast multipole methods (FMM). A reference for these methods is Gumerov & Duraiswami (2004).