VIEILLISSEMENT STATIQUE ET DYNAMIQUE ET MODELISATION DU COMPORTEMENT DES ALLIAGES AA5083-H116 ET AA5182-0

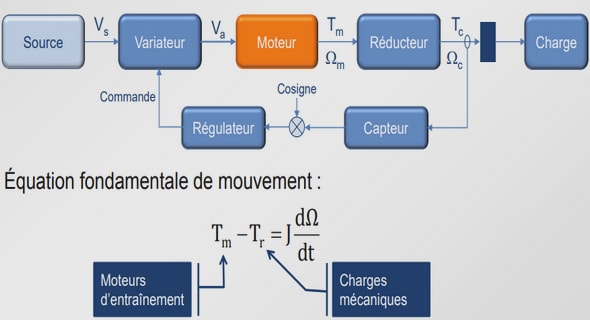
VIEILLISSEMENT STATIQUE ET DYNAMIQUE ET MODELISATION DU COMPORTEMENT DES
ALLIAGES AA5083-H116 ET AA5182-0

Cadre thermodynamique général de l’élasto-viscoplasticité

Dans cette section, on décrit très brièvement le cadre maintenant classique de l’élasto viscoplasticité en petites déformations qui sera utilisé ici pour modéliser le comportement des alliages d’aluminium avec prise en compte des phénomènes de vieillissement.

Partition des déformations

On se place dans le cadre de l’hypothèse de partition de la déformation totale ε εε ε en une déformation élastique e εε ε ε (réversible) et une déformation inélastique p ε ε ε = + εε ε ε (permanente), e p (6.14) Chapitre 6 – Prise en compte des phénomènes de vieillissement statique et dynamique du comportement des alliages AA5083-H116 et AA5182-O

Choix des variables thermodynamiques

Les variables thermodynamiques ou variables indépendantes sont les variables observables, la déformation totale ε εε ε et la température Τ, et les variables internes décrivant l’état actuel du matériau : p ε εε ε , K V . En faisant un découplage entre l’élasticité et la visco plasticité, l’énergie libre dépend de la déformation élastique, de la température et des variables internes K V (Lemaitre et al., 2009) : ( , , ) p K T ψ ψ = − V ε ε ε ε ε ε ε ε (6.15) La contrainte, l’entropie et les forces thermodynamiques associées aux variables internes K V sont obtenues par les lois d’état ε et T (ρ est la masse volumique) : ψ ρ ∂ = ∂ σ σσ σ ε εε ε s T ψ ∂ =−∂ K K ψ ρ ∂ = ∂ A V (6.16) 6.3.3 Domaine d’élasticité.

Lois d’évolution des variables internes. Ecoulement et écrouissage Pour décrire le comportement dans le domaine de la viscoplasticité, on définit d’abord un domaine d’élasticité dans l’espace des contraintes, domaine à l’intérieur duquel aucune déformation viscoplastique n’est possible. Celui-ci est défini par une fonction de charge ( , ; ) K K f A V σ σσ σ telle que 0 0 p f < → = ε εε ε (6.17) Lorsque 0 f ≥ , il y a déformation viscoplastique et on a la loi d’écoulement p λ = P ε εε ε (6.18) où Pdésigne la direction de l’écoulement viscoplastique et λ son amplitude. En l’absence de relation de cohérence comme en plasticité indépendante du temps, λ doit être définie.

Les résultats expérimentaux montrent que cette amplitude dépend de la distance du point de chargement au domaine d’élasticité et on prend généralement ( ) f λ=Φ (6.19) où Φ est une fonction positive à dérivée positive pour obtenir une sensibilité positive à la vitesse de déformation. Au cours de la déformation viscoplastique, le domaine d’élasticité peut se déplacer, changer de taille, tourner ou même se déformer, permettant ainsi la description des phénomènes d’écrouissage.

Les lois d’évolution des variables internes sont aussi de la forme K K λ = V P s’il ne s’agissait que d’évolution avec la déformation plastique. Mais pour prendre en compte les éventuels effets du temps, tels que par exemple la restauration ou le vieillissement faisant l’objet de ce travail, les lois d’évolution des variables internes ont la forme assez générale K K K + λ = V P Q 

Le deuxième terme décrivant les phénomènes régis par le temps. 6.4 Particularisation. Loi de viscoplasticité classique pour les métaux Dans le cas des matériaux métalliques comme l’aluminium considéré dans ce travail, et dans le cas où l’on néglige la distorsion du domaine d’élasticité, il est coutume d’utiliser, en plus de la déformation plastique p εε ε ε , deux variables internes pour d’écrire l’écrouissage de ces matériaux.

La première, r, de nature scalaire représente l’écrouissage isotrope (changement de taille du domaine d’élasticité) alors que la seconde,α αα α , de nature tensorielle décrit l’écrouissage cinématique (déplacement du domaine d’élasticité dans l’espace des contraintes. Du point de vue physique, ces variables d’écrouissage sont associées, d’une part, à la densité de dislocation et, d’autre part, aux incompatibilités des déformations visco-plastiques au sein du polycristal.

La variable d’écrouissage isotrope r sera généralement croissante, sauf intervention éventuelle du processus de restauration. En cas de chargement cyclique la variable cinématique α αα α , au contraire, n’évoluera pas de façon monotone. Une variable courante pour décrire l’écrouissage isotrope est la déformation plastique cumulée p définie par t p= 0 ε p 2 ( ): ( ) 3 τ ε