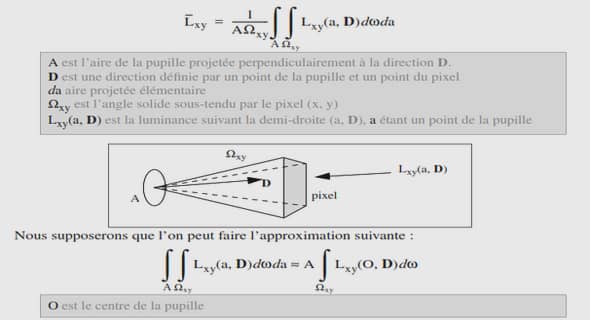
Théorème du point fixe de Banach Picard

Le Théorème du Point Fixe de Picard dit qu’une contraction d’un espace métrique complet a un point fixe unique. Ce théorème donne un comportement régulier du point fixe par rapport aux paramètres. De plus, il fournit un algorithme d’approximation du point fixe comme limite d’une suite itérée. Mais d’une part, montrer que la fonction contractante peut entraîner de laborieux calculs. D’autre part, les conditions sur la fonction et l’espace étudiés restreignent le nombre de cas auxquels on peut appliquer le théorème. Définition 1.3.1. (Point fixe) Soient (E, ||.||E) un espace de Banach, et T : E → E une application. On appelle point fixe de T tout point x ∈ E tel que T x = x. Ce qui est équivalent à dire que l’équation : T x − x = 0

Définition 1.3.2. 

Soit (X, D) deux espaces métriques, une application T : X → D est dite lipschitzienne s’il existe une constante α > 0 telle que : ∀(x, y) ∈ (X × D), dD(T x, T y) ≤ αdX(x, y)

Remarque 

Tout application α lipschitzienne est uniformément continue sur son domaine de définitions. 2. Avec les hypothèses précédentes, on dit que T est contractante si T est α lipschitzienne avec une constante α ∈]0, 1[. Théorème 1.3.1. (Schauder)([9]) : Soient E un espace de Banach et Q ⊂ E un convexe et compact. Alors toute application continue T : Q → Q possède un point fixe. Théorème 1.3.2. ([9]) Soient X un espace métrique complet et T une applications contractante de X, alors : il existe dans X un unique point fixe x, c’est-à-dire T x = x. Si x0 est un point quelconque de X, pour tout entier n on a la suite xn+1 = T xn est appellée la suite itérative de Picard. 

Existence et approximation de solutions pour des applications non expansives 

Définition 1.4.1. Une application non expansive d’un espace normé est une applications α lipschitzienne tell que α = 1. Définition 1.4.2. Soit K un sous-ensemble non vide d’un espace linéaire normalisé réel E et soit T : K → K une application. T est non expansive si ||T x − T y|| ≤ ||x − y|| (1.5) Remarque : Bien que les applications non expansive sont des généralisations de contractions, ils sont des applications contractive. Plus précisément, si K est un sousensemble fermé non vide d’un espace de Banach E et T : K → K une application non expansive qui n’est pas une contraction, alors, comme le montre l’exemple suivant, T peut ne pas avoir un point fixe. Exemple 1.4.1. : 1. Considérons l’intervalle unitaire [0, 1] avec la norme habituelle. La fonction T donné par la formule T x = 1 − x pour tout x a un point fixe unique, x ∗ = 1 2 mais, sauf pour le cas trivial x0 = 1 2 , l’itération Picard commençant à partir de x0 donne une suite d’oscillation. 2. Soit la fonction f(x) = √ x 2 + 1 sur X = [0, 1]. X est fermé dans R, et complet car R est complet.

Remarque

 Le théorème (1.4.1) ne fournit aucune information sur l’approximation d’un point fixe de T. De l’exemple 1, nous voyons que l’itération Picard ne résout pas cette situation, en général. De ce fait, plusieurs autres procédures d’itération en point fixe ont été envisagées. Les plus courantes seront définies dans la suite en fonction de leur utilisation. 

Définition 1.4.3.

Soit K un sous-ensemble convexe d’un espace linéaire normé E et soit T : K → K une application. Étant donné un x0 ∈ K et un nombre réel λ ∈ [0, 1] ; x0 ∈ K, la suite xn définie par la formule : xn+1 = (1 − λ)xn + λT xn, n = 0, 1, 2, … (1.6) est généralement appelée itération Krasnoselskij, ou itération Krasnoselskij–Mann. Clairement, (1.6) se réduit à l’itération de Picard (1.2) pour λ = 1. Pour un x0 ∈ K, la suite xn définie par la formule xn+1 = (1 − λn)xn + λnT xn, n = 0, 1, 2, … (1.7) où {λn}n ⊂ [0, 1] est une suite de nombres réels satisfaisant à certaines conditions appropriées, est appelée une itération de Mann. Remarque : Il a été démontré par Krasnoselskij [20] dans le cas où λ = 1 2 , et plus tard par Schaefer [24] pour un arbitraire λ ∈]0, 1[, que si E est un espace de Banach uniformément convexe et K est un sous-ensemble convexe et compact de E ( et donc, par le théorème (1.4.1), T a des points fixes), alors l’itération de Krasnoselskij converge vers un point fixe de T. De plus, Edelstein [14] a prouvé qu’une stricte convexité de E suffit pour la même conclusion. La question de savoir si l’hypothèse de convexité stricte peut être supprimée a été répondu par l’affirmative par Ishikawa [18] par le résultat suivant. Théorème 1.4.2. Soit K un sous-ensemble d’un espace de Banach E et soit T : K → K une application non expansive où a et b sont des nombres réels tels que 0 ≤ a ≤ b < 1. Pour un x0 ∈ K arbitraire, considérons le processus d’itération de Mann, {xn}n donné par (1.7) sous les hypothèses suivantes : (a) xn ∈ K pour tous les entiers positifs n ; (b) 0 ≤ λn ≤ b < 1 pour tous les entiers n ; (c) P∞ n=0 λn = +∞ ; si {xn} est borné, alors xn − T xn → 0 quand n → +∞. Théorème 1.4.3. ([9]) Soit K un sous-ensemble d’un espace linéaire normé réel X et soit T une application non expansive de K vers X. Supposons que pour x0 ∈ K, il existe une suite {xn}n ⊆ K qui est bornée.