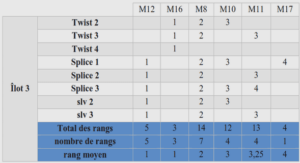
Temps minimal pour la contrôlabilité exacte locale

In particular, this definition requires that arbitrarily small motions may be done with arbitrarily small controls.In this introduction, we first recall two previous results concerning local controllability of systems similar to (2.1). We present a positive result in arbitrary time and a setting for which there exists a positive minimal time. Then, we present the main results of this article i.e. we give a precise setting where local controllability hold in time larger than a minimal time and fails otherwise. We end by a short bibliography and by setting some notations. Finally, let us summarize the proof of Theorem 2.1 in [16]. This proof relies on the linear test (see [54, Chapter 3.1]), the inverse mapping theorem and a regularizing effect. In particular, the assumption (2.7) is necessary for the linearized system to be controllable in H On the other hand, Coron proved in [53] that this local controllability does not hold in arbitrary time: contrary to Theorem 2.1, a positive minimal time is required for the local controllability. Precisely, Coron proved the following statement.and K = 1. In particular, Theorem 2.3 applies to the particular case studied by Coron in [53]. Thus, the variables (s, d) are not required in the state for the minimal time to be positive. Moreover, the control u does not need to be small in L.

Finally, we summarize the proof of Theorem 2.4. Under assumption (2.13), only a finite number of the coefficients hµϕ the ground state is not controllable along a finite number of directions. We will see that all of these directions are recovered at the second order. Moreover, all these directions excepted one, present a rotation phenomena in the complex plane, for the null input solution. This idea of using a power series expansion and exploiting a rotation phenomena was first used on a Korteweg-de Vries equation by Cerpa and Crépeau in [44]. However, their strategy has to be adapted in our situation, because one lost direction does not exhibit a rotation phenomenon (see Remark 2.3).The first controllability result for bilinear Schrödinger equations such as (2.1) is negative and proved by Turinici [134], as a corollary of a more general result by Ball, Marsden and Slemrod [5]. Then, it has been adapted to nonlinear Schrödinger equations in [86] by Ilner, Lange and Teismann. Because of such noncontrollability results, these equations have been considered as non controllable for a long time. However, progress have been made and this question is now better understood.

Temps minimal pour la contrôlabilité exacte locale

Concerning exact controllability issues, local results for 1D models have been proved in [10, 11] by Beauchard; almost global results have been proved in [15], by Coron and Beauchard. In [16], Beauchard and Laurent proposed an important simplification of the above proofs. In [53], Coron proved that a positive minimal time may be required for the local controllability of the 1D model. In [12], Beauchard studied the minimal time for the local controllability of 1D wave equations with bilinear controls. In this reference, the origin of the minimal time is the linearized system, whereas in the present article, the minimal time is related to the nonlinearity of the system. Exact controllability has also been studied in infinite time by Nersesyan and Nersisyan in [113, 114].Now, we quote some approximate controllability results. Mirrahimi and Beauchard proved in [17] the global approximate controllability, in infinite time, for a 1D model and in [103] Mirrahimi proved a similar result for equations involving a continuous spectrum. Approximate controllability, in finite time, has been proved for particular models by Boscain and Adami in [1], by using adiabatic theory and intersection of the eigenvalues in the space of controls. Approximate controllability, in finite time, for more general models, have been studied by three teams, with different tools: by Boscain, Chambrion, Mason, Sigalotti [45, 25, 30], with geometric control methods; by Nersesyan [111, 112] with feedback controls and variational methods; and by Ervedoza and Puel [70] thanks to a simplified model.