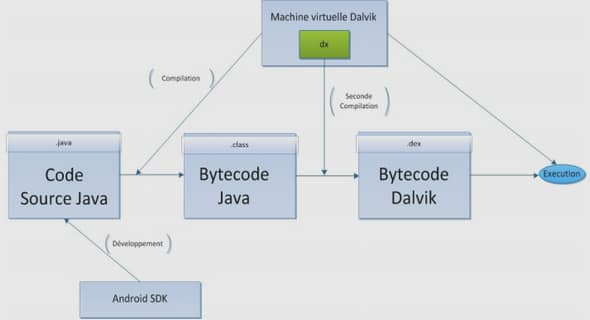
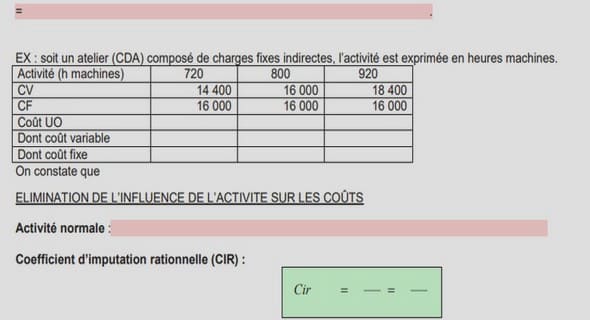
Simulation en espace libre

Dans le présent chapitre, nous présentons une application du krigeage sur des données simulées en espace libre. Dans la première section, nous décrivons les données d’exposition radioélectrique, générées à l’aide d’EMF Visual et on calculer les variogrammes expérimentaux. Par la suite, une étude géostatistique concernant les corrélations spatiales des données et les comportements des variogrammes à grandes distances et à l’origine est réalisée. Dans la seconde section, nous présentons des techniques d’échantillonnage. Dans la troisième section, on présente une application de la méthode du krigeage ordinaire sur les données sélectionnées à partir de données d’espace libre (données simulées par EMF Visual). Enfin, nous montrons les résultats d’application de cette méthode sur des nouveaux jeux de données: échantillons à partir des simulations électromagnétiques en prenant en compte les propriétés diélectriques des réflecteurs. (400*400*50 m3), et installé dix-huit antennes omnidirectionnelles à des altitudes différentes (entre 14-28m). Le positionnement de ces antennes a été effectué de sorte que l’on trouve une distribution des antennes similaire à une distribution réelle. La simulation est réalisée en espace libre. La Figure 7.1 montre la scène de simulation ou les points roses présentes les positions des antennes; les objets (bâtiments, voiture,…) sont des objets décoratifs et leurs propriétés diélectriques ne sont pas prises en compte dans cette simulation, seul le sol a été pris en compte. La quantité obtenue est la densité de puissance exprimée en (W/m2).

Sur la Figure 7.3, nous présentons les résultats des simulations pour les deux fréquences 900 MHz et 1800MHz. Ces résultats représentent la densité de puissance calculée sur un plan (xoy) avec z = 2m. Ce plan est partitionné en grille régulière de taille (81*81) avec un pas de 5 m (Figure 7.2). La densité de la puissance est évaluée à chaque sommet de la grille. variogramme qui quantifie la corrélation entre les données par classes des distances. Sur la Figure 7.4, nous avons calculé le variogramme expérimental des données pour chaque fréquence. Les valeurs du variogramme expérimental se stabilisent autour de valeurs de 0.014 et de 0.0125 pour les deux fréquences de respectivement 900 MHz et 1800 MHz. L’existence de ce palier permet de conclure que l’intégralité de la variabilité spatiale a été observée. Nous venons d’examiner le comportement du variogramme à grande distance. Il est également très utile d’étudier son comportement pour de petites valeurs de h, puisqu’il est relié à la continuité et à la régularité spatiale de la variable. La Figure 7.5 illustre les comportements des variogrammes 900MHz et 1800MHz au voisinage de l’origine. Pour les deux fréquences, nous extrapolons vers l’origine en supposant un comportement parabolique, tel qu’il est donné par le modèle de Cauchy de paramètre p=2, avec la présence d’une petite structure de portée 15m pour 900MHz et de 18 m pour 1800MHz.

 Pour ajuster ces variogrammes expérimentaux, nous avons utilisé le modèle de variogramme de Cauchy (5.14), ce modèle a été développé par [35] pour les données de magnétisme et de gravimétrie, un autre modèle de variogramme est calculé par [52] pour des données d’électromagnétisme dans un environnement fermé (chambre réverbérante). Sur la Figure 7.6, nous présentons l’ajustement des variogrammes au voisinage de l’origine. Dans le deux cas étudiés, nous avons ajusté chaque variogramme expérimental par un modèle de Cauchy. Pour les deux fréquences, nous avons un comportement particulier de la densité de la puissance sur un voisinage local, qui peut être représenté par un disque de rayon 20m. Dans ce disque nous avons des petites variations d’exposition, qui peuvent s’expliquer par les présences des petites zones homogènes dues à l’interférence d’exposition des antennes. Ces zones homogènes normalement seront plus larges dans le cas de la présence d’obstacles à cause des phénomènes de réflexions et diffractions multiples sur ces obstacles, ce qui sera examiné dans la dernière section de ce chapitre. Sur la Figure 7.7, nous présentons l’ajustement des variogrammes à grande distance. Chacun des modèles à été ajusté par un double structure de Cauchy; une petite structure pour la modélisation de la variation à petite distance, la portée de cette petite structure étant de 15 m et 22 m respectivement pour 900 MHz et 1800MHz, et une structure de Cauchy de longue portée, de 116m et 153m respectivement pour les deux fréquences. Nous avons fait varier la puissance p du modèle pour bien ajuster les modèles expérimentaux; dans les deux cas, nous arrivons à un ajustement avec une puissance p = 2.