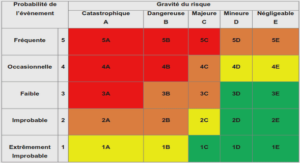
Self-adaptive Spectrum Management in Partially Observable Environments

Due to the recent and dramatic development of the wireless communication industry, the demand for wireless spectrum has been growing rapidly. Thus, the spectrum scarcity is becoming a challenge for several recent studies. Both academic and industry are rec- ognizing that traditional fixed spectrum allocation is very inefficient, such that most of the time the bandwidth that was allocated is not optimally used and the corresponding channel is idle, which forms spectrum holes [8]. CR [1], which is a new paradigm for de- signing wireless communication systems, appeared in order to enhance the utilization of the radio frequency spectrum. It was considered as the key technology that enables SUs to access the licensed spectrum. Typically, SUs access opportunistically the spectrum when it is not used by PUs. The presence of several SUs in the same portion of spectrum band enhanced the need to efficiently share the spectrum. Indeed, the utilization of the radio spectrum is reduced due to collisions among SUs under decentralized channel se- lection schemes. In order to optimize the utilization of the scarce spectrum resources, DSA become a promising approach to increase the efficiency of spectrum usage and to solve the scarcity problem. Surprisingly, the impact of the energy constraint, due to the limited mobile users’ bat- tery, and the capacity of CR to support additional QoS were somehow ignored and not sufficiently studied in the literature. In many wireless systems, it is very important to provide reliable communications while sustaining a certain level of QoS. However, chal- lenges in providing the QoS assurances increase due to the fact that SUs operate under constraints on the licensed channels’ occupancy, and competition between each other.

We investigate an important problem for determining the OSA mechanism, and we propose a general model that allows us to study the impact of energy consumption and expected delay on the OSA policy. The main novelty of our approach is to consider a POSG framework. The theory of POMDP was widely and successfully used, like in [80], [53] and [90], to model and build OSA mechanisms in CR networks. However, those works do not consider the competition between SUs. Very few works proposed to model such competition(see [94] and [95] for example). Moreover, those works do not have significant results. In fact, using a DP approach to solve a POMDP is possible by transforming it into a completely observable MDP over belief states [95]. It is very difficult to generalize this technique for POSG as the SUs may have different beliefs. This problem was alleviated by introducing the notion of generalized belief state in [41], however the optimal algorithm becomes intractable beyond a small horizon. In our work, we focus on the existence of an SNE between SUs. The SNE is solved using a Linear Program (LP). Second, we identify paradoxical behaviors of SUs. One of the observed paradoxes here is a kind of Braess paradox, a well-studied paradox in routing context [96]. Our paradox indicates that decreasing the spectrum occupancy may lead degradation of the performance in term of the average throughput for SUs. This observation is due to the increase of the aggressiveness of SUs when the spectrum availability increases. We look further for a network control mechanism in order to optimize the average throughput of SUs at the SNE. For this end, we consider a Stackelberg game formulation [97].Note that Stackelberg game formulations was already proposed in the CR literature (see for example [39], [40] and [98]), as the natural hierarchy between PUs and SUs is very similar to the hierarchy between leaders and followers. Nevertheless, it was not used in order to enhance the network usage. In the second part of this chapter, we propose a control mechanism, for the network manager using a Stackelberg game formulation, such that the total average throughput of the SUs is maximized in this partially observable environment.n- ear programming solvers for MDP, which are able to handle finite and infinite horizon problems. Moreover, authors of [101] considered a problem similar to ours but in a queueing context. They used the linear programming in order to solve an MDP and to study the equilibria for N players scenario in a stochastic game context. Few works fo- cused on how SUs should operate in order to satisfy some QoS requirements and energy constraints. Authors of [53] incorporated the energy constraint in the design of the op- timal OSA policy, in a single user context, and formulated their problem as a POMDP. The major difference between this work and ours is that the authors do not considered the competition between SUs. In [102], the authors presented a queueing analysis of a CR with multiple SUs. They proposed an adaptive algorithm to find the optimal contention probability that minimizes the expected delay. Authors of [103], proposed an energy-efficient non-cooperative strategy for resource allocation in CR networks based on a game theoretical approach.