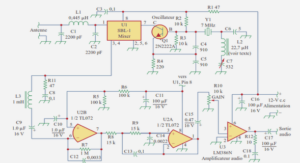
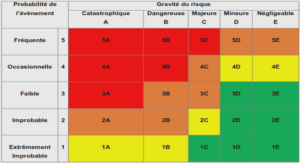
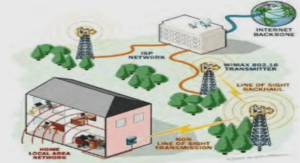
Robot types

Industrial robots can be classified according to several criteria, but the most common is their architecture (the arrangement and types of their joints). The most popular members of this classification are articulated robots, Cartesian robots, SCARA robots, cylindrical robots, spherical robots and parallel robots (mostly, so-called Delta robots).

Six-axis articulated robots are the most commonly used robots in industrial applications. The advantages of articulated robots are their wide versatility and high flexibility (Hanafusa et al., 1981). Some parallel robots are considered to have better accuracy and larger payload capacity (Filion, 2015). Delta robots are known for their fast-parallel movements. SCARA robots are generally used in assembly tasks (Urrea et al., 2016).

Robot calibration and error sources 

Finding better robot parameters different from the nominal model represents a calibration procedure to decrease the absolute position error of industrial robots. These errors are caused by geometric and non-geometric sources inside the robot model. There are three levels of calibration which are defined according to these error sources. A level-1 calibration improves the joint level errors, where level-2 calibration includes every geometric error source into consideration (Conrad et al., 2000). The level-3 model takes non-geometric stiffness errors into account in addition to other levels. (Gong et al., 2000).

Geometric errors 

Geometric errors are caused by machining and assembly tolerances. These are the DenavitHartenberg (DH) parameters, i.e., the link lengths, twists and offsets, and the joint offsets. For example, the joint offsets are caused by unavoidable errors in the installation of the joint encoders with respect to the joint reference (zero) position. The geometric errors also include errors in the base and tool reference frames. According to Judd and Knasinski (1990), geometrical errors have the most prominent effects on the complete robot position accuracy.

Non-geometric errors 

Non-geometric errors are considered as all other variations. The most common example is the stiffness of the gearboxes (generally modeled as linear). However, other non-negligible examples are the stiffness of the robot links and the thermal expansion of the robot components.

Level-1 calibration 

Level-1 calibration (also called mastering) aims at correcting the offsets that happen at the robot joint level. These offset parameters have the most significant impact on accuracy improvement, according to Heping et al. (2008), when calibrating a six-axis articulated robot.

Indeed, every robot manufacturer provides procedures for mastering the robot, and these need to be executed every time the robot’s battery is dead.

Level-2 calibration

Level-2 calibration identifies every geometrical error parameter from the robot’s kinematic model. This level of calibration includes the error modification of joint level (Level-1) calibration.

To date, numerous level-2 calibration experiments have been performed using different mathematical models. Differences in equations and parameters between kinematic modeling methods affect the accuracy when performing level-2 calibration. In the case of articulated robots, Hayati (1983) is an example of the studies covering all kinematic parameters with a specific modeling method.

Level-3 calibration 

Non-geometrical errors are improved in Level-3 calibration. Usually, for successful accuracy improvement, all calibration levels are combined to identify geometrical and non-geometrical error parameters. Various dynamic modeling principles have been implemented throughout this level of calibration to complete the robot identification model.

The Newton-Euler algorithm was used by Khosla and Kanade (1985) to identify the joint stiffness coefficient exerted through moments and forces. Thermal expansion related parameters were identified by Gong et al. (2000) through observing the changes related to the effect of thermistor sensors. Nubiola and Bonev (2013) and Feng et al. (2013) uses a torsional spring model to identify the joint stiffness parameters, and Lightcap et al. (2008) uses an additional cubic spring coefficient implemented to the same model for its identification. An elasto-geometrical calibration model was presented by Kaveh et al. (2016) identifies the nongeometric error parameters by observing multidirectional external loads applied to the joints.

Absolute vs. relative accuracy 

According to Whitney et al. (1986), robot accuracy is targeted through forward or inverse, absolute and relative calibration approaches. Relative accuracy is targeted to calibrate the robot with respect to a user reference frame defined through a set of joint values. Li et al. (2018) experimented calibration with a parallel robot for relative accuracy achievement by defining the user frame through reflector sensors fixed on the robot end-effector. Absolute calibration aims to improve absolute accuracy by defining a world reference frame with respect to the robot base’s actual location. The parameters concerning the world reference frame with respect to the robot base frame are also taken into identification. Nubiola and Bonev (2013) calibrated a robot with six degrees of freedom by defining the reference frame by placing and measuring three spherical mounted retroreflectors (SMR) with a laser tracker.