Représentation des systèmes temps réel

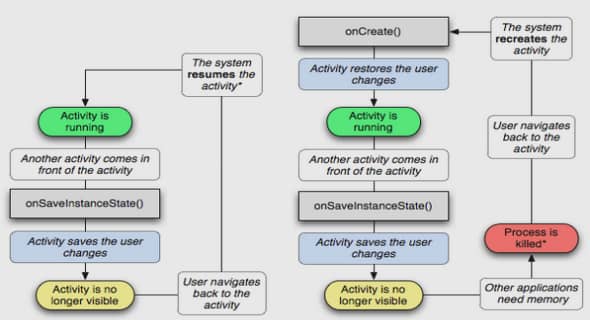
Représentation des systèmes temps réel

Nous distinguons entre le temps réel strict et le temps réel souple. Pour un système temps réel strict*, aucun dépassement d’échéance n’est toléré. Il s’agit là des systèmes critiques pour lesquels une défaillance peut avoir des conséquences graves. Dans un système temps réel souple*, le dépassement de certaines contraintes temporelles est ac ceptable dans la mesure où la qualité du service fourni par l’application est correcte.

Cette qualité de service peut par exemple s’exprimer par une borne maximale sur le dépassement des échéances [LA10]. Il s’agit des systèmes de visioconférence, ou en core de jeux en réseau. Comme nous l’avons introduit dans la section 1.1, nous nous focalisons sur l’étude des systèmes temps réel stricts. Lorsqu’on étudie l’ordonnancement d’un système temps réel, il est primordial de spécifier les hypothèses qui sont faites sur ce système.

Notamment, il convient de spé cifier les modèles considérés car l’analyse du système dépend de ces modèles. Il existe différents modèles de tâches, ainsi que différents modèles de plates-formes multipro cesseurs. Nous présentons ici les modèles couramment rencontrés dans la littérature en précisant ceux que nous considérons dans ce manuscrit.

Modèles de tâches Modèle d’activation

L’analyse d’unsystèmetempsréelimpliquelaconnaissancedumodèled’activation des tâches. Trois modèles sont couramment rencontrés dans la littérature. Le premier est celui des tâches apériodiques. Une tâche apériodique est une tâche pour laquelle la période d’activation n’est pas connue. Il est donc difficile d’analyser de manière stricte un système composé de ce type de tâches sans faire d’hypothèse sur la probabilité de leur arrivée.

Les deux autres modèles d’arrivée sont respectivement ceux des tâches sporadiques* et des tâches périodiques*. La durée séparant deux activations d’une tâche i est appelée période* dans le cas où i est une tâche périodique. Dans le cas où i est une tâche sporadique, la durée séparant deux activations n’est pas fixe. Néanmoins, la période minimaleentre deuxactivations est connue, ce qui permetdepouvoiranalyser ces tâches dans le pire cas.

Cette période d’inter-arrivé minimale* est, par souci d’homo généité avec le modèle périodique, couramment appelée période. La période d’une tâche i constitue un de ses paramètres temporels et nous la notons Ti. Nous portons notre attention sur l’étude des tâches sporadiques et des tâches périodiques. Le lecteur intéressé par la gestion des tâches apériodiques dans les systèmes temps réel pourra toutefois se reporter entre autres à la thèse de Masson [Mas08].

Instance

Unetâchepériodique(ousporadique)correspondàl’exécutiond’unensembled’ins tructions qui se répète. Afin de distinguer les différentes occurrences d’une même tâche, nous employons le terme d’instance* d’une tâche (aussi appelée requête). Nous notons Jik la kième instance de la tâche i en commençant la numérotation à 1.

Ainsi, la première instance de la tâche 1 est donc notée J11. Lorsque nous faisons référence à une instance quelconque de la tâche i, nous notons celle-ci Ji. Instant d’activation L’instant d’activation* d’une tâche est l’instant auquel une instance de cette tâche est prête à être ordonnancée. L’instant d’activation d’une tâche correspond à un décalage par rapport à une origine des temps fixée à l’instant t = 0.

L’instant d’activation d’une instance est appelé release time dans la littérature anglophone. Nous notons par consé quent cet instant d’activation rik pour l’instance Jik et ri pour une instance quelconque Ji. Nous notons Oi l’instant d’activation de la première instance de la tâche i. Dans le cas d’une tâche périodique, l’instant rik est défini par rik = Oi + (k 1)Ti