Regularity of the American put option in the Lévy’s exponential model with general discrete dividends

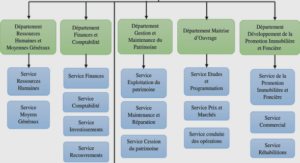
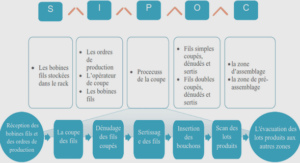
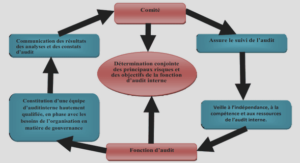
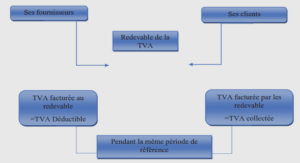
Regularity of the American put option in the Lévy’s exponential model with general discrete dividends

We analyze how we can approximate the value function near the dividend dates. We analyze the regularity of the value function and of the optimal exercise boundary of the American Put option when the underlying asset pays a discrete dividend at known times during the lifetime of the option. The ex-dividend asset price process is assumed to follow the exponential Lévy dynamics and the dividend amount is a deterministic function of the ex-dividend asset price just before the dividend date.

This function is assumed to be non-negative, non-decreasing and with growth rate not greater than 1. Under some explicit conditions, we prove that the exercise boundary is continuous at any time but the dividend dates. Introduction This chapter is organized as follows. In the first section, we give the notations and assumptions used in the following sections.

The second section is devoted to the statement of the American option problem in the framework of discrete dividends. We will assume that its value is given by the Snell envelop of some process, and we will state some first results derived from [JJ12] and [LM08], especially the fact that the exercise region is fully characterized by a time-dependent curve called the exercise boundary.

In the third section, we give conditions for this last one to be continuous. A necessary and sufficient condition for the smooth fit to hold is given in the fourth section. The last section deals with a numerical procedure to get the price of the American option in our model

American option Statement of the problem

We consider the American put option with maturity T > 0 and strike K > 0 written on an underlying stock S. We assume that the stochastic dynamics of the ex-dividend price process of this stock can be modelled by the exponential Lévy model which generalizes [JJ12] where the dynamics is given by the Black-Scholes model. However, we consider the same modelling for the payment of dividends.

At deterministic times 0 ≤ tI d < tI−1 d < ··· < ti d < ··· < t1 d < T, this stock is paying discrete dividends. At each dividend time ti d, the value of the stock becomes Sti d = Sti d− − Di Sti d− where Di(Sti d−) is 4.2 American option 57 the value of the dividend payment. For each i ∈ {1,…,I}, the function Di is supposed to be a natural dividend function, and we define ρi(x) = x −Di(x). We then abusively refer to A1 as the assumption that each dividend function is natural and we will assume that this assumption is always fulfilled in the next sections.

In the financial market which consists of both financial assets S and cash discounted at rate r, we know at least in the Black-Scholes model (cf [Myn92]) that Pt = ess h sup τ∈FS:t≤τ≤T E e−r(T−t)(K − ST)+|FS t i is an arbitrage-free value. From now on we state that the price of the American put option is Pt. Following the construction of [JJ12], we build recursively the functions ui. We recall that u0 is the pricing function of the standard American put option with strike K,

in the Lévy’s exponential model described in Section 4.1. For results on u0, we will refer to [LM08]. We then set t0 d = T, and for i ≥ 0, θi d = ti d − ti+1 d , in order to define for i ≥ 1 : ui : (θ,x) ∈ R2 + 7→ sup τ∈FX ≤θ 4.2.2 First results E e−rτ K−xeXτ +1{τ<θ}+1{τ=θ}ui−1(θi−1 d ,ρi(xeXθ)) (4.3) We insist on the fact that notations are the same as in [JJ12] up to the fact that ¯ Sx t = xeXt.We state the results of [JJ12] which can be extended without big modifications.

Any modification will be enlighted. Some of the new arguments rely on results of [LM08]. As we can factorize the initial condition, we can state this first lemma : Lemma 4.2.1 (Lemma 3.2.2 of [JJ12]) For i ≥ 0 and θ ≥ 0, the mappings x 7→ x+ui(θ,x) and x 7→ −ui(θ,x) are non-decreasing, or equivalently, x 7→ ui(θ,x) is 1-Lipschitz and non-increasing. By a plain induction on Equation (4.3), for any (θ,x) ∈ R2+, (K − x)+ ≤ ui(θ,x) ≤ K.

The following Lemma needs a proof for the sake of completeness. Lemma 4.2.2 The mapping (θ,x) ∈ R⋆+ ×R+ 7→ ui(θ,x) ∈ R+ is bounded and continuous. Proof. We have already mentionned that 0 ≤ ui ≤ K. We now prove the continuity. We recall that a Lévy process is stochastically continuous and thus for any bounded continuous function f one has trivially limt→0 E[f(Xt)] = f(0). Since we have already established Lemma 4.2.1,

one just needs to prove the continuity in θ for any x ≥0. Let ε > 0, by definition of ui, for any n ≥ 0, it exists τn ε ∈ FX θ such that by setting xn = nε : 58 4 Regularity of the American put option in the Lévy’s exponential model with general discrete dividends ui(θ, xn) − ε ≤ E e−rτn ε K −xneXτn ε +1{τ<θ} +1{τn ε=θ}ui(0,xneXθ