Réalisation pratique d’un amortisseur à raideurs ajustables

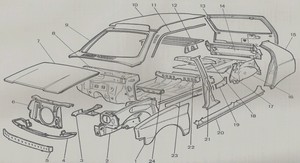
Après avoir présenté l’influence du NLTVA sur un profil d’aile en flottement, nous nous proposons d’étudier dans ce chapitre une réalisation expérimentale possible et originale d’un NLTVA. L’idée principale du dispositif présenté ici est de tirer partie de la force magnétique présente entre des aimants permanents. Le dispositif proposé est appelé absorbeur magnétique de vibration et noté MVA dû à sa dénomination anglaise. Le MVA est schématisé sur la Figure 7.1. Ce chapitre est composé de travaux menés conjointement avec Simon Benacchio lors de son stage post-doctoral à l’Unité de Mécanique de Février à Septembre 2015. Ce travail a donné lieu à une publication parue dans la revue Nonlinear Dynamics (numéro 2 de juillet 2016). Le chapitre est composé de cette publication et un résumé détaillant le MVA est donné en préambule. L’idée du MVA a été originalement proposée par Jean Boisson, qui a étudié sa faisabilité avec un étudiant au début de l’année 2014. Puis, j’ai aidé à la conception du MVA utilisé pour les essais statiques servant à mesurer sa force de rappel, à la réalisation de ces essais statiques, puis à l’établissement et à la validation du modèle utilisé pour estimer la force de rappel du MVA. Le MVA, schématisé sur la Figure 7.1, est composé d’un assemblage d’aimants annulaires positionnés sur des axes en plastique. Hormis l’aimant numéroté 1 sur la Figure 7.1, qui peut se mouvoir le long de son axe, tous les aimants sont fixes. Les aimants 2 et 3, positionnés sur l’axe central, et nommés aimants répulsifs, ont une polarisation opposée à celle de l’aimant mobile 1. Ces deux aimants ont pour but de repousser l’aimant central afin de le maintenir au milieu de son axe et ainsi créer une force de rappel. Les aimants désaxés 4, 5, 6 et 7, appelés aimants correctifs, ont la même polarisation que l’aimant mobile 1. Ces quatre aimants correctifs ont pour rôle de modifier la force de rappel exercée par les aimants 2 et 3. Les paramètres géométriques de ce dispositif sont la distance d entre les axes, la distance 2 R entre les aimants correctifs du même axe, la distance r entre l’aimant mobile 1 au repos et l’amant fixe 3, et enfin la position x de l’aimant mobile, comme montré sur la Figure 7.1. La force de rappel appliquée à l’aimant mobile est alors de la forme K1 x + K3 x 3 pour des faibles valeurs de x, où les raideurs K1 et K3 dépendent des propriétés des aimants ainsi que des deux longueurs d et R. À l’aide de ce dispositif, il est alors théoriquement possible de modifier la raideur linéaire et cubique du MVA indépendamment l’une de l’autre. Ce qui est particulièrement intéressant dans le cadre du NLTVA où les raideurs linéaire et cubique doivent être accordées indépendamment. Réalisation pratique d’un amortisseur à raideurs ajustables 120 Chapitre 7 Réalisation pratique d’un amortisseur à raideurs ajustables Le champ magnétique des aimants est modélisé à l’aide d’une expansion multipolaire. La force d’interaction entre les aimants, et donc la force de rappel du MVA, découle du champ magnétique. Des essais de traction statiques sont réalisés afin de valider la modélisation retenue pour estimer la force de rappel du MVA. Pour la généralité de l’étude, trois situations sont mises en avant. Une première où la raideur linéaire du MVA est positive, qui correspond au cas du NLTVA, une deuxième où la raideur linéaire est nulle, qui correspond au cas du NES et une trosième où la raideur linéaire est négative, ce qui donne un amortisseur bi-stable. Une fois la modélisation de la force de rappel du MVA effectuée, son comportement dynamique est étudié à la fois expérimentalement et numériquement. Les trois situations décrites précédemment sont traitées. Dans les trois cas, les résultats expérimentaux et numériques sont en très bon accord.

Design of a magnetic vibration absorber with tunable stiffnesses

1 Introduction The vibration mitigation of mechanical structures is a long-standing problem which receives a considerable and continuous interest due to its importance in engineering applications. The most famous vibration absorber is the linear tuned-mass damper (TMD), originally proposed by Frahm [11] and theoretically studied by Den Hartog [8]. Whereas the original work by Ormondroyd and Den Hartog [33] considered the primary structure (PS) as a linear undamped oscillator, further research extended their results to a damped oscillator as PS, in order to derive the optimal parameter values for a given set of optimisation criteria [3,40,48]. The extension of these results to flexible structures having an infinite number of modes is also a topic for current research, see e.g. [24]. The drawbacks of the TMD as a vibration absorber are well known and documented. The main associated problem is related to the narrow bandwidth of optimal control, asking for an accurate tuning which must continue over times. In the last decades, a number of investigations have been conducted in order to over123 S. Benacchio et al. come these limitations, one of the main ideas being to use a nonlinearity in order to improve the vibration absorber design. The concept of a nonlinear energy sink (NES) relies on a vanishing linear stiffness, giving rise to an essentially nonlinear restoring force. Having no natural frequency, the NES can thus adapt itself to the frequency of the PS [12,41,44]. A targeted energy transfer (TET) can then occur in an irreversible fashion [42,43]. The concept has been demonstrated theoretically and experimentally in a series of papers [13,15,25–27,31,32]. As also remarked by a number of investigators, the frequency range over which a linear passive vibration isolator is effective may be limited by the mount stiffness required to support a static load. Hence, the idea of selecting the eigenfrequency of the vibration isolator as small as possible leads to the concept of “quasi-zero stiffness” (QZS) absorber, which has been studied both theoretically and experimentally [5,6,23,46]. Another idea which has emerged recently is to use the nonlinearity of the absorber in order to control the nonlinearity of the primary structure. As remarked in [45], a TMD is less effective as soon as the PS is nonlinear and exhibits typical features of nonlinear dynamics. In this context, an extension of den Hartog’s equal peak method has been proposed in [18], leading to the definition of a nonlinear tuned vibration absorber (NLTVA), which can be used e.g. for suppressing the limit cycle oscillations in a Duffing–Van der Pol system [19]. A recognised drawback of the NES is that a sufficient energy level is required for the targeted energy transfer to occur [42,43]. Recent studies have considered the case of a negative linear stiffness, leading to a bi-stable vibration absorber device. For example, it has been shown in [29,37] that such a vibration absorber may be more efficient than an NES as the energy barrier for activation is smaller in the bi-stable case