Quelle approche pour le Transport à la Dem

De l’optimalité d’une solution

Un cas représentatif de TAD

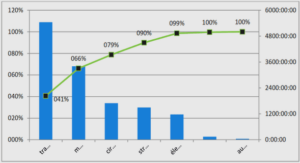
À travers cette section, nous introduisons les concepts d’optimum et d’optimisation dans le cadre d’un problème de TAD classique. Dans l’exemple de la figure 2.1, quatre clients se rendent au même endroit (D) pour le même horaire et nous cherchons une solution pour les transporter. Selon la politique de desserte appliquée, la solution « optimale » varie en fonction des critères adoptés. Le tableau 2.1 présente trois solutions, chacune optimale pour un objectif plutôt : – économique : puisque l’utilisation de véhicules supplémentaires engendre un surcoût, nous n’en utilisons qu’un pour prendre en charge tous les clients. Cependant, l’économie réalisée se fait au détriment de la qualité de service. En effet, les retards cumulés sont très grands (70 minutes) par rapport aux temps théoriques de parcours ; – de qualité de service au client : en affretant trois véhicules, les clients acheminés ne souffrent d’aucun retard, par-contre le cumul des temps de parcours augmente, engendrant une plus forte émission de polluants (CO2) et le coût économique du service fait plus que tripler (nombre de véhicules plus le carburant) ; – environnemental : la troisième solution réduit le cumul des temps de parcours (65 minutes) pour limiter l’émission de polluants. Néanmoins, cette solution accuse un léger retard (5 minutes) et nécessite deux véhicules.

Quels objectifs ?

Si nous plaçons ces trois objectifs à égalité et que nous les optimisons concurremment, les trois solutions présentées sont équivalentes puisque chacune d’entre elles maximise (ou minimise) un objectif en particulier. Il appartient finalement à l’AOT (Autorité Organisatrice des Transports) de décider de la solution à mettre en œuvre. Pour cela, nous proposons d’orienter notre recherche de solutions au TAD en fonction de trois objectifs : – minimiser le nombre de véhicules : objectif économique; – minimiser les temps de parcours : objectif environnemental ; – minimiser les retards : objectif de qualité de service. Ces objectifs sont contraints par : – le nombre de véhicules ; – les horaires ; – la tolérance des clients vis-à-vis des retards occasionnés. Le problème d’optimisation de transport de personnes est bien connu en informatique, qui est mise à contribution pour pallier les très fortes complexités (cf. annexe B) de ces problèmes. C’est l’objet de la section suivante. Aussi, les méthodes d’optimisation que nous proposons, sont associées au « dial-aride problem » qui vise à optimiser les tournées. 

Les grands problèmes de tournées 

Dans sa formalisation, le TAD appartient à la famille des problèmes de tournées très étudiés en recherche opérationnelle. Nous ne définissons pas une taxonomie exhaustive des problèmes de tournées étudiés en informatique, mais nous en rappelons les principaux qui ont trait au TAD. Nous commençons par un rappel du problème du voyageur de commerce, qui est à la base de tous les problèmes de tournées. Pour étudier ces différents problèmes de tournées, nous nous basons nécessairement sur la théorie des graphes (cf. annexe A), où le problème de desserte est représenté par un graphe G, dont les sommets représentent les différents points de passage du problème. Soit G = (S, E) un graphe tel que : – S = {xi}, avec i ≤ |S|, |S| = p le nombre de sommets du graphe G, xi un sommet du graphe G ; – E = S × S, l’ensemble des arêtes du graphe G

Le problème du voyageur de commerce 

Le problème du voyageur de commerce (Travelling Salesman Problem, TSP), déjà étudié par Kruskal (1956) et Flood (1956), consiste à visiter un ensemble de villes une seule fois en revenant au point de départ, tout en minimisant la distance parcourue. Départ et arrivée de la tournée sont confondus mais ne sont pas fixés préalablement à l’instar de l’exemple de la figure 2.2.1. 

Exemple de TSP avec cinq communes

la tournée (b) n’est pas optimale tandis que la tournée (c) minimise la distance parcourue. Dans sa forme de base, le TSP ne dispose que d’un seul véhicule (autrement dit un seul chemin), mais l’on peut travailler avec n véhicules. C’est le n-TSP, qui consiste à minimiser la somme linéaire des distances parcourues par chacun des n véhicules v ∈ V (V est l’ensemble des véhicules) qui se partagent la visite de l’ensemble des villes : min n ∑ v∈V p ′ ∑ a∈F da Le TAD est d’un niveau de complexité plus grand puisque les clients montent dans le véhicule à un arrêt pour descendre à un autre et que la qualité de service entre en ligne de compte. A B D C E 2.47 2.2 3.51 1.84 (a) Longueurs : 8.18 et 3.68 A B D C E 2.2 2.21 1.49 2 (b) Longueurs : 4.0 et 5.9 A B D C E 1.3 2 1.84 2.2 (c) Longueurs : 5.14 et 4.4 FIG. 2.3: Exemple de 2-TSP avec cinq communes (A, B, C, D et E) : la tournée (c) est optimale car elle minimise la somme linéaire des distances parcourues par les deux véhicules. 

Les problèmes de tournées

 Pourtant très étudiés en informatique à en juger l’importante littérature consacrée à leurs sujets, les problèmes de tournées ne disposent pas de définitions académiques génériques. Cependant, trois problèmes semblent constituer l’essence même des problèmes de tournées et de leurs variantes, transportant marchandises ou individus, applicables au TAD. Ces problèmes, souvent assimilés au Dial-a-Ride Problem (DARP) pour le transport de personnes, ou encore au Pick-up and Delivery Problem (PDP) pour les marchandises, se différencient en problèmes plus spécifiques répondant à des objectifs précis sous contraintes. Ainsi, une première généralisation des problèmes de tournées a été proposée par Savelsbergh et Sol (1995), qui classe le DARP comme un sous-problème du General Pick-up 36 2.2. Les grands problèmes de tournées and Delivery Problem qui cherche les meilleures tournées sans correspondance répondant à un ensemble de requêtes de transport, chacune étant définie par sa charge, son origine et sa destination. De cette définition générale découlent trois sous-problèmes, très étudiés en informatique et en recherche opérationnelle : 1. Le Pick-up and Delivery Problem, où chaque requête de transport spécifie une origine et une destination uniques et où tous les véhicules partent et reviennent en un dépôt central ; 2. Le Vehicle Routing Problem (VRP), qui est un PDP dans lequel toutes les origines ou toutes les destinations se confondent avec le dépôt central ; 3. Le Dial-a-Ride Problem, qui est quant à lui, un PDP où l’on considère des personnes, i.e. d’un point de vue formel, une charge à transporter vaut 1 et cette charge peut avoir un rôle dans la recherche d’optimalité (qualité de service pour le voyageur). Une fois cette taxonomie de base établie, les variantes possibles de ces sous-problèmes se distinguent notamment dans les contraintes posées à la résolution : nombre et capacités des véhicules (contraintes physiques inviolables), temps de parcours et de desserte (contraintes temporelles, potentiellement transgressables selon la tolérance octroyée). Ces tolérances suggèrent la mise en place de fenêtres de temps : des marges temporelles situées sur les prises en charge et/ou dessertes, ou sur le parcours total, qui offrent aux véhicules une tolérance dans la réalisation de leurs parcours, comme par exemple le VRP with time windows (Bräysy et Gendreau, 2005). Puis viennent toutes les considérations relevant de la qualité de service, c’est-à-dire les souhaits exprimés par le client, comme le temps qu’il est prêt à accorder à son voyage. Ces considérations permettent éventuellement des détours pour prendre en charge d’autres marchandises ou clients, jouant sur l’élasticité des fenêtres de temps et sur les temps de parcours ou délais de livraison souhaités. Regardons maintenant plus en détail le transport de personnes que constitue le DARP, qui est à la base du TAD.

 Le Dial-a-Ride Problem

 Le DARP consiste en l’organisation et la conception de tournées de véhicules pour n utilisateurs requérant chacun leur propre lieu de prise en charge et leur propre lieu de desserte. Dans sa version de base, le DARP est résolu avec une flotte de véhicules identiques, ayant tous les mêmes caractéristiques et le même dépôt. L’objectif de ce problème consiste à planifier une tournée en répondant au mieux aux souhaits des usagers (qualité de service, durées des courses) tout en minimisant les coûts de fonctionnement (nombres de véhicules et de chauffeurs nécessaires…). Un exemple classique d’utilisation est le service de transport de personnes de « porte-à-porte » (Diana et Dessouky, 2004), où la recherche opérationnelle peut aider à parachever ces objectifs en fournissant des solutions fiables à coûts réduits. Dans le cadre de notre étude, nous ne considérons pas les dépôts des véhicules. Il ne s’agit pas là d’une volonté de simplifier le problème, mais il faut bien comprendre que le TAD ne fonctionne pas comme un transport de type ambulance qui revient systématiquement à son hôpital de rattachement. En effet, les véhicules peuvent demeurer au dernier arrêt desservi en attendant la prochaine course. De plus, si nous tenons compte des densités des demandes de transport, nous pouvons envisager que les zones de desserte correspondent également à des zones de départ. Aussi, le concept de dépôt ne constitue pas un élément clé de notre application. Également, se pose le problème du prépositionnement des véhicules qui constitue une recherche en soi et que nous ne traitons pas dans cette thèse.