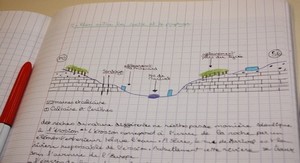
PROJET D’EXTENSION DU PERIMETRE BAS MANGOKY

– Transmission du G0 de station : Figure II-7. Transmission de G0 de station La transmission du G0 de station est un autre mode de transmission des gisements basé sur le G0moyen de la station de départ. Si on calcule un G0moyen de station au départ du cheminement, on peut calculer le G0 de station en chaque sommet j par transmission du G0. En stationnant au sommet j, on peut écrire : G0j = Gij + (200 – Lrj) Au sommet i, on peut écrire : Gij = G0i + Lvi – 400 Donc : 𝐺0𝑗 = 𝐺0𝑖 + 𝐿𝑣𝑖 − 𝐿𝑟𝑗 − 200 NB : – Si le résultat est négatif, ajouter 400 gon. – S’il est supérieur à 400 gon, retrancher 400. d – Fermeture angulaire d’un cheminement encadré : Les données sont : A, B, C et D, donc aussi GAB noté Gd, et GCD noté Gf. On calcule de proche en proche tous les gisements de tous les côtés pour arriver au gisement d’arrivée GCD connu qui sert de contrôle des erreurs de lecture d’angles. Figure II-8. Cheminement encadré  On peut écrire : 𝐺𝐵1 = 𝐺𝐴𝐵 + 𝐻𝑔𝐵 − 200 𝐺1−2 = 𝐺𝐵1 + 𝐻𝑔1 − 200 Etc. 𝐺′𝑓 = 𝐺3𝐶 + 𝐻𝑔𝐶 − 200 G′f est le gisement d’arrivée observé (G′CD) Si l’on fait la somme de ces équations membre à membre, on obtient : 𝐺′𝑓 = 𝐺𝑑 + ∑(𝐻𝑔𝑗) − (𝑛 + 1) .200  n étant le nombre de côtés de la polygonale.  Σ (Hgj) représente la somme de tous les angles de gauche. Si le résultat G′f est négatif, ajoutez 400 gon autant de fois nécessaires. L’erreur de fermeture angulaire fa est alors la différence entre ce gisement de fermeture observé et le gisement de fermeture théorique GCD, noté Gf, issu des coordonnées des points connus C et D. 𝑓𝑎 = 𝐺′𝑓 − 𝐺𝑓 e – Fermeture angulaire d’un cheminement avec transmission de G0 Figure II-9. Cheminement encadré avec transmission d’un G0moyen de station Sur le cheminement de la Figure II-9, la position du zéro du limbe à chaque station a été dessinée, de même que toutes les lectures angulaires. Pour se ramener à une transmission de gisement, il suffit de considérer que : – Le G0 de départ au point B est une visée sur un point B′ fictif qui se trouverait dans l’alignement du zéro du limbe. La lecture arrière LrB de B sur B′ est égale à 0. Donc l’angle de gauche en B a pour valeur HgB = LvB – LrB = LvB ; P – Le G0 d’arrivée au point C est une visée sur un point fictif C′. La lecture avant sur le point C′ est égale à zéro, l’angle de gauche au point C vaut HgC = LvC – LrC = – LrC Le Gisement de départ est alors : 𝐺𝑑 = 𝐺0𝐵 − 200 Le Gisement d’arrivée observé est : 𝐺′𝑓 = (𝐺0𝐵 − 200) + ∑𝐻𝑔𝑖 − (𝑛 + 1) . 200 Avec HgB = LvB et HgC = – LrC Le gisement d’arrivée « exacte » est de : 𝐺𝑓 = 𝐺0𝐶 Et la fermeture angulaire est toujours : 𝑓𝑎 = 𝐺′𝑓 − 𝐺𝑓 f – Tolérance sur la fermeture angulaire : Soit σa l’écart type angulaire par station dépendant de l’appareil utilisé ; on obtient comme tolérance angulaire Ta pour un cheminement de n côtés : – Pour un cheminement fermé : 𝑇𝑎 = 2,7 . 𝜎𝑎 . √𝑛 – Pour un cheminement encadré : 𝑇𝑎 = 2,7 . 𝜎𝑎 . √𝑛 + 1 g – Compensation angulaire : C’est l’opération qui consiste à répartir l’écart de fermeture angulaire sur tous les angles observés. On ne peut compenser angulairement un cheminement que si l’écart de fermeture angulaire est inférieur à la tolérance réglementaire. Si ce n’est pas le cas, la manipulation doit être reprise en entier car il s’agit d’une faute. 

Nivellement directe 

Le nivellement direct, appelé aussi nivellement géométrique, consiste à déterminer la dénivelée ∆HAB entre deux points A et B à l’aide d’un appareil : le niveau et d’une échelle verticale appelée mire. 

Principe 

La mire est placée successivement sur les deux points. L’opérateur lit la valeur ma sur la mire posée en A et la valeur mb sur la mire posée en B. La différence des lectures sur mire est égale à la dénivelée entre A et B. Cette dénivelée est une valeur algébrique dont le signe indique si B est plus haut ou plus bas qu’A (si ∆HAB est négative alors B est plus bas qu’A). La dénivelée de A vers B est : ∆𝐻𝐴𝐵 = 𝑚𝑎 − 𝑚𝑏 La dénivelée de B vers A est : ∆𝐻𝐵𝐴 = 𝑚𝑏 − 𝑚𝑎 L’altitude HA d’un point A est la distance comptée suivant la verticale qui le sépare du géoïde (surface de niveau 0). Si l’altitude du point A est connue, on peut en déduire celle du point B par : 𝐻𝐵 = 𝐻𝐴 + ∆𝐻𝐵𝐴 Figure II-10. Principe de base du nivellement direct La portée est la distance du niveau à la mire ; elle varie suivant le matériel et la précision cherchée, et doit être au maximum de 60 m en nivellement ordinaire et 35 m en nivellement de précision. Dans la mesure du possible, l’opérateur place le niveau à peu près à égale distance de A et de B (sur la médiatrice de AB, Figure II-10. Principe de base du nivellement direct) de manière à réaliser l’égalité des portées.

Lecture sur mire 

La mire est une échelle linéaire qui doit être tenue verticalement (elle comporte une nivelle sphérique) sur le point intervenant dans la dénivelée à mesurer. La précision de sa graduation et de son maintien en position verticale influent fortement sur la précision de la dénivelée mesurée. La mire classique est généralement graduée en centimètre. La chiffraison est souvent en décimètre. Le réticule d’un niveau est généralement constitué de quatre fils : – Le fil stadimétrique supérieur (s´), qui donne une lecture m1 sur la mire ; – Le fil stadimétrique inférieur (s), qui donne la lecture m2 sur la mire ; – Le fil niveleur (n), qui donne la lecture m sur la mire ; – Le fil vertical (v), qui permet le pointé de la mire ou d’un objet.La lecture sur chaque fil est estimée visuellement au millimètre près. Pour chaque lecture, il est judicieux de lire les trois fils horizontaux de manière à éviter les fautes de lecture : on vérifie en effet, directement sur le terrain, que : 𝑚 = 𝑚1 + 𝑚2 2 .