Power-Based Control Algorithms

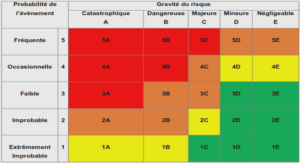
Topology Management

Neighbor Discovery 

The performance of both ad hoc and mesh networks depend on the interaction among communicating entities in a given neighborhood. Thus, in general, before a node starts communicating, it must discover the set of nodes that are within its direct communication range. Once this information is gathered, the node keeps it in an internal data structure so it can be used in dierent networking activities such as routing. The behavior of an ad hoc node depends on the behavior of its neighboring nodes since it must sense the medium before it starts transmitting packets to nodes in its interfering range, which can cause collisions at the other nodes. Node discovery can be achieved with periodic transmission of beacon packets (active discovery) or with promiscuous snooping on the channel to detect the communication activity (passive discovery). In probe-based distributed protocol for knowledge range adjustment (PRADA) [75], a given source node periodically sends a discovery packet to its neighboring nodes, to which the latter reply with a location update packet (that might include, for instance, the node’s geographical location). PRADA adjusts dynamically its communication range, called topology knowledge range, so it leads to a faster convergence of its neighboring nodes

Packet Forwarding Algorithms

 An important part of any multi-hop network is the packet forwarding algorithm that chooses which neighboring node is going to be used to forward the data packet. It does so following a forwarding goal, having the shortest average hop distance from source to destination for instance. In this case, the set of potential nodes may include only those within direct communication range of the current node or also all nodes along the route to the destination. The forwarding goal may also include some QoS parameters such as the amount of energy available at each node. The following forwarding algorithms consider only nodes that are in direct communication range of the node that has a data packet to be forwarded, as depicted in Figure 6.1. The Most Forward within Radius (MFR) forwarding algorithm [86] chooses the node that maximizes the distance from node S to point p. In this case, as depicted in Figure 6.1, it is node 1. On the other hand, the Nearest Forward Progress (NFP) forwarding algorithm [102] chooses the node that minimizes the distance from node S to point q. In this case it is node 2. The Greedy Routing Scheme (GRS) [55] uses the nodes’ geographical location to choose the one that is closest to the destination node D. In this case it is node 3. The compass selected routing (COMPASS) algorithm [44] chooses the node that minimizes the angle α but considering the 4 nodes that are closest to node D. In this case it is node 4. The random process forwarding algorithm [81], as the name suggests, chooses a random node that is in direct communication range from S. The Partial Topology Knowledge Forwarding (PTKF) algorithm [75] chooses a node using a localized shortest path weighted routing where routes are calculated based on the local topological view, taking into consideration the transmission power needed to transmit on that link.

Classication 

Broadly speaking, topology control algorithms for ad hoc networks can be classied as having a hierarchical or clustering organization, or a power-based control organization [11] [110]. Furthermore, these algorithms can be either centralized, distributed, or localized. 

Clustering Algorithms 

The clustering process consists in dening a cluster-head node and the associated communication backbone, typically using a heuristic. The goal is to 90 Chapter 6 Topology Management Figure 6.1: Strategies used by some forwarding algorithms avoid redundant topology information so that the network can work more eciently. Clustering algorithms are often modeled as graph problems such as the Minimum Connected Dominating Set (MCDS) [49]. This problem asks for the minimum subset of nodes V 0 in the original graph G = (V, E) such that V 0 forms a dominating set of G and the resulting sub-graph of the MCDS has the same number of connected components as G. In other words, if G is a connected graph, so is the resulting sub-graph. MCDS is a NP-complete problem [48], and thus, we must look for approximate solutions. In the case of the clustering algorithm, nodes in the dominating set represent the cluster-heads and the other nodes are their neighbors. An inherent characteristic of an ad hoc network, which makes this problem much more dicult, is that its topology is dynamic. The cluster heads can be selected using either deterministic or non-deterministic approaches: • A deterministic solution is similar to a distributed synchronous algorithm in the sense that it runs in rounds. In this case there is just one round, and after nishing it the cluster-heads are chosen. Suppose we have a node and its neighboring nodes, i.e., its one-hop neighborhood. The lowest ID solution selects the node with the lowest identier among these neighbors to create the Minimal Dominating Set (MDS) [48], whereas the max degree solution selects the node with the highest degree [65] [97]. The MOBIC solution examines the variations of RSSI (Received Signal Strength Indicator) signal among them to 6.4 Further readings 91 select the cluster-head . • A non-deterministic solution runs multiple incremental steps to avoid variations in the selection process and to minimize conicts among cluster-heads in their one-hop neighborhood. Examples of this approach are CEDAR [97], SPAN [29], and solutions based on a spanning tree algorithm .

Power-Based Control Algorithms

 A mobile node in a MANET needs an energy source (typically a battery) to be able to execute all its tasks. Batteries need to be recharged to provide a continuous energy supply for a node. To extend the lifetime of nodes in an ad hoc network, we need algorithms to determine and adaptively adjust the transmission power of each node so as to meet a given minimization goal and, at the same time, maintain a given connectivity constraint. Some possible minimization goals are control the maximum or average power and dene a maximum or average connectivity degree. Some connectivity constraints are a simplex communication or a full-duplex communication (biconnected). Ramanathan and Hain [86] propose a topology control algorithm that dynamically adjusts its transmission power such that the maximum power used is minimized while keeping the network biconnected. 6.4 Further readings The literature on topology control is vast, eventhough it is mainly devoted to ad hoc and sensor networks. In fact, one can nd a wide range of good proposals, to solve specic problems, introductory surveys and books dedicated to this subject that can give a broader and deeper view of the subject. Good surveys are the works of Rajaraman [85] and Santi . Two good books devoted to topology control are the works of Santi  and Labrador.