Optimisation des paramètres par simulation

L’optimisation des paramètres par simulation est une solution possible pour le dimensionnement du SYSMFS en minimisant une fonction coût (Équation (85)). En principe, il s’agit d’une comparaison des solutions obtenues par la simulation qui partagent le même schéma conceptuel. En étudiant l’effet de certains paramètres sur la réponse obtenue, les meilleures solutions seront déterminées. Les algorithmes d’optimisation offrent en général l’avantage de l’économie de temps en réduisant le nombre d’essais (simulations) nécessaires en vue d’obtenir une valeur optimale de la réponse. Ils conviennent normalement à un large éventail d’applications et ils utilisent des techniques diverses pour la recherche d’optimum : le gradient conjugué, la recherche stochastique, les stratégies d’évolution, etc. Pendant une optimisation, le calcul de la fonction coût demande généralement beaucoup plus de temps de calcul que le temps requis pour déterminer les valeurs suivantes dans une itération d’optimisation ; ce principe est valable pour toutes les procédures d’optimisation dans les problèmes de simulation des bâtiments. En premier lieu, le gain de temps total d’une optimisation se fait donc au niveau de la simulation ; un nombre assez important des solutions est possible afin d’optimiser le déroulement de la simulation (type de solveur, hypothèse de modèle, etc.). Ensuite, c’est à l’algorithme d’optimisation de réduire efficacement le nombre des simulations en réalisant un avancement maîtrisé vers la valeur optimale de la fonction coût ; ce dernier devrait alors réduire le nombre des simulations inutiles, sans pour autant s’arrêter sur des optimums locaux. La performance d’un algorithme d’optimisation prend en compte les valeurs optimales trouvées, le nombre des simulations effectuées par chaque méthode ainsi que toutes autres informations supplémentaires données par l’algorithme suite à l’optimisation. Dans la suite de ce travail, deux algorithmes d’optimisation sont testées pour leurs performances : un algorithme hybride GPS-PSO et un algorithme basé sur les plans d’expériences. Le premier algorithme est déjà implémenté dans un code d’optimisation générique [22] tandis que pour le deuxième nous avons créé les procédures et l’implémentation. Chaque algorithme est testé avec une fonction de test et avec le modèle SYSMFS ; une comparaison de ces deux méthodes est également présentée dans ce chapitre. 

Types des variables à optimiser 

Les paramètres à optimiser peuvent être soit de type discret, soit de type continu (§1.2.2). Les panneaux solaires sont constitués de plusieurs modules interconnectés entre eux, chaque module ayant une surface prédéfinie par le fabricant. Nous considérons cependant que la surface totale des panneaux peut varier librement dans la gamme [5, 50] m² ; pour respecter la consigne précédente, la valeur obtenue de surface doit être alors arrondie à 0,5 m² près. Les ballons de stockage thermique sont, quant à eux, fabriqués principalement dans des séries standardisées de volumes ; il est possible cependant de commander des ballons sur mesure. En utilisant l’Équation (32), le volume du ballon peut être considéré comme une variable continue avec des valeurs prises dans la fourchette [25, 3000] L. 

Valeurs initiales des paramètres à optimiser 

Certains algorithmes d’optimisation (ex. gradient conjugué) sont plus influencés par les valeurs initiales des paramètres à optimiser que d’autres algorithmes. Suivant le domaine d’application et l’algorithme employé, certaines valeurs initiales peuvent rendre la convergence plus rapide vers un optimum potentiel, qu’il soit local ou global. En revanche, d’autres valeurs initiales peuvent retarder la convergence en éloignant l’algorithme de la zone optimale pour certain temps avant que la convergence commence. Une connaissance préalable du comportement de la fonction coût pour une application donnée pourrait éventuellement venir en aide dans le choix des valeurs initiales des paramètres à optimiser. Dans ce but, l’étude paramétrique menée précédemment avec la surface de réponse (Figure 3.20) est indispensable. 

Méthodes de test pour les algorithmes d’optimisation étudiés 

L’objectif principal de notre étude est de tester le concept d’optimisation par plans d’expériences pour le dimensionnement optimal des systèmes comme les SYSMFS. L’application de la méthode d’optimisation par plans d’expériences est une nouveauté car, selon notre connaissance, elle n’a pas été utilisée auparavant pour l’optimisation du dimensionnement par la simulation des systèmes solaires comme les SSC ou les SYSMFS. Le benchmark de ces méthodes est réalisé pour deux cas : une fonction de Rosenbrock et le modèle SYSMFS.De cette manière, nous validons la méthode OptDOE et nous comparons sa performance avec d’autres méthodes d’optimisation (Tableau 4.1). 

Fonction de Rosenbrock

Introduite par Rosenbrock en 1960, la fonction de Rosenbrock est une fonction non convexe de deux variables qui est souvent utilisée dans le domaine des problèmes d’optimisation pour tester la performance des algorithmes. Elle est définie par (Figure 4.2) : (87) Le minimum global de la fonction de Rosenbrock se trouve à (1,1), où la valeur de la fonction est nulle. Ce minimum est situé à l’intérieur d’une vallée de forme parabolique longue et étroite. Les algorithmes d’optimisation peuvent facilement trouver la vallée, mais la convergence vers le minimum global est d’une difficulté considérable. Sur le contour de cette fonction (Figure 4.2, b), nous présentons les points initiaux que nous avons choisis et à partir desquels nous testons les algorithmes d’optimisation. 

Modèle de SYSMFS 

La forme de la réponse du modèle SYSMFS a été présentée précédemment dans le Chapitre 3. Cette surface (Figure 3.20) constitue une base de comparaison pour les deux algorithmes d’optimisation qui seront appliqués ultérieurement au même modèle.

Optimisation par l’algorithme hybride GPS-PSO 

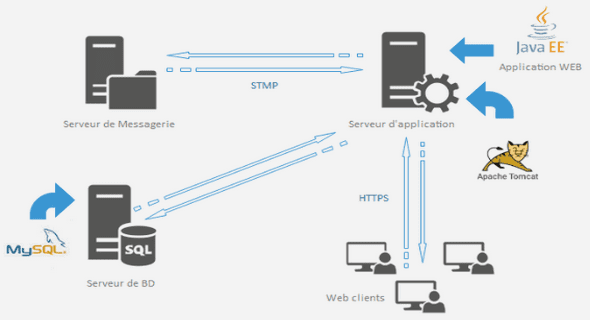
Dans le 0, une brève description a été faite des deux algorithmes individuels qui constituent l’optimisation hybride GPS-PSO. Le logiciel d’optimisation générique GenOpt intègre plusieurs algorithmes d’optimisation différents. Pour les problèmes de simulations propres au bâtiment, l’algorithme hybride a été déjà utilisé dans la littérature avec un logiciel de simulation des bâtiments [80]. Le couplage entre notre modèle SYSMFS développé avec TRNSYS et le logiciel d’optimisation est relativement direct. La Figure 4.3 illustre le schéma de couplage entre les deux logiciels. L’échange des données entre les deux logiciels se fait avec des fichiers au format texte simple. Les résultats obtenus par cette méthode sont comparés avec ceux issus de l’étude paramétrique afin d’en savoir plus sur la performance de cette méthode d’optimisation.