Modélisation géométrique de la transformation

Interprétation qualitative de l’allure des courbes

L’allure particulière des courbes cinétiques et le fait que les pressions de gaz correspondant à l’équilibre thennodynamique du système ne soient pas très élevées (1,8. HP Pa de monoxyde d’azote à 500 C pour une pression d’oxygène de 2500 Pa (cf. tableau IY.1.)), nous ont conduits à rechercher une intetprétation des courbes expérimentales s’appuyant sur des raisons à la fois thennodynamiques et cinétiques. Les observations de microscopie électronique en transmission (paragraphe 11.6.) semblent indiquer que l’on retrouve du baryum dans l’ensemble des particules du mélange calciné à 500 C, dès le début de la réaction.

De plus, le titanate de baryum apparaît partout dans les particules, et non pas particulièrement autour ou à proximité du nitrate de baryum. Cela pourrait s’expliquer par une diffusion superficielle très rapide des espèces, car les expériences sont réalisées à une température proche de la température de fusion du nitrate de baryum. Chaque grain de dioxyde de titane serait ainsi immédiatement recouvert des éléments de structure du nitrate de baryum, qui se retrouveraient donc répartis dans l’ensemble des particules du mélange. Compte tenu de l’influence très fortement inhibitrice du monoxyde d’azote sur la transformation, nous avons supposé qu’elle pouvait être due à un effet d’abord thermodynamique puis cinétique des gaz.

Nous avons donc cherché à évaluer la quantité de monoxyde d’azote produite au cours de la perte de masse initiale, et la pression qui en résulterait si ce gaz restait confmé à l’intérieur du volume poreux de la poudre. Celui-ci a été déterminé par porosimétrie au mercure, il vaut 601 mm3/g. La répartition du volume poreux est donnée en Annexe A.4. La perte de masse initiale (8 % environ) permet d’évaluer à 1,52.10-3 mole/g le nombre de moles de monoxyde d’azote produites par gramme de poudre, au cours de cette perte de masse.

La réaction commencerait très rapidement entre le dioxyde de titane et les éléments de structure du nitrate de baryum répartis dans l’ensemble de la poudre, puis ralentirait du fait de pressions locales fortes au niveau des agglomérats du mélange, et ce, jusqu’à ce que le monoxyde d’azote s’évacue et que la pression à l’intérieur de l’échantillon s’équilibre avec celle fixée dans l’atmosphère de calcination (ou du moins devienne inférieure à la pression d’équilibre thermodynamique). La réaction pourrait alors reprendre, conduisant au second maximum de vitesse.

L’augmentation de la pression extérieure de monoxyde d’azote diminuant le gradient de pression entre l’intérieur et l’extérieur de la poudre. elle défavorise la diffusion du gaz dans les particules et donc retarde la reprise de la réaction. La première partie de la réaction se déroule donc dans des conditions non isobares et non isothermes (la réaction étant endothermique), la seconde partie de la réaction, correspondant à la partie des courbes située entre les deux maxima de vitesse, se fait dans des conditions isothermes mais non isobares; enfin. la dernière partie (après le second maximum de vitesse) est isotherme et isobare.

Seul ce dernier cas est prévu par les modèles, aussi avons-nous tenté d’interpréter cette partie des courbes par un modèle géométrique classiquement utilisé dans le cas des réactions solide-solide. Ce modèle conduit en effet à une vitesse constamment décroissante en fonction du temps, ce qui est bien le cas expérimentalement dans la partie des courbes considérée. 

Modélisation géométrique de la fin de la transformation

Les hypothèses

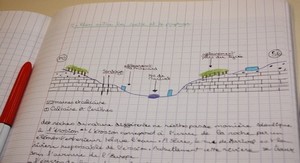
A un instant donné de la transformation, la situation du mélange peut être schématisée de la façon représentée sur la figure N.32. En effet, nous savons que le titanate de baryum se forme à l’intérieur des grains de dioxyde de titane, ces grains peuvent être approximés à des sphères (cf. la micrographie de la figure IV.21a.). Figure IV.32. développement de la couche sphérique de titanate de baryum à l’intérieur des grains de dioxyde de titane. Pour modéliser la transformation, nous ferons l’hypothèse que les éléments de structure du nitrate de baryum sont répartis autour des grains de dioxyde de titane, et que la germination de la nouvelle phase est infiniment rapide.

Nous supposerons donc que la transformation, dans les conditions isobares et isothermes dans lesquelles s’appliquera le modèle géométrique, est limitée par une diffusion chimique à travers la couche de titanate de baryum formée. Nous supposerons de plus que cette diffusion est stationnaire, et que les réactions aux interfaces sont instantanées et constamment à l’équilibre, les concentrations des espèces diffusantes à ces interfaces étant donc fixées par des équilibres. Nous supposerons enfin que tous les grains du mélange ont un comportement identique, de façon à pouvoir raisonner sur un seul grain.