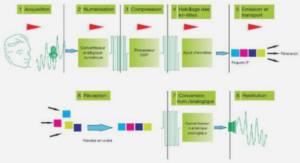
MODÉLISATION ÉCONOMÉTRIQUE DES DÉTERMINANTS DE LA SURVIE DES ENTREPRISES

L’analyse non-paramétrique

Pour traiter d’une façon descriptive la durée d’un phénomène donnée (vie et mort, emploi et chômage …), on fait généralement recours à la méthode d’estimation nonparamétrique, qui vise à faire une exploration des données au cours du temps. Le terme non-paramétrique, comme le définissent Le Goff et Forney (2003), répond à deux conditions : 1) aucune hypothèse n’est posée sur la distribution du risque au cours du temps (Courgeau et Lelièvre 1989, Allison 1995), c’est-à-dire qu’à un instant donné, le risque est estimé de manière totalement indépendante de celui estimé à l’instant précédent ; 2) aucune hypothèse n’est faite sur les différences de rythme d’occurrence des événements au cours du temps entre diverses sous-populations. Pour cela, deux méthodes d’estimation non-paramétriques existent, à savoir la méthode d’estimation de Kaplan-Meier (KM), et la méthode d’estimation actuarielle. « L’usage de la première méthode est particulièrement indiqué lorsque l’on dispose de données portant sur un faible effectif ou pour lesquelles l’unité de temps considérée dans la mesure des durées est petite (par exemple, le mois dans le cas des événements sociodémographiques). En revanche, cette méthode est à déconseiller si de nombreux individus connaissent l’événement à chaque instant ou bien encore si les durées ont été mesurées en utilisant une unité de mesure du temps qui est large, par exemple, l’année. Il devient alors plus indiqué d’utiliser les méthodes d’estimation actuarielle » (Le Goff et Forney, 2003, p. 3).

Les tests non-paramétriques

Pour comparer la survie de deux ou plusieurs sous-populations, il existe une grande variété de tests statistiques portant sur la fonction de survie, appelés des tests non-paramétriques. Le principe de ces tests, est qu’ils ne font aucune hypothèse sur la distribution sous-jacente des données. « Ils permettent de prendre en compte toute l’information sur l’ensemble du suivi sans la nécessité de faire des hypothèses sur la distribution des temps de survie » (Alberti et al., 2005). Plusieurs tests sont proposés dans la littérature : le test du Log-Rank (MantelHaenszel, 1959), le test de wilcoxon (Gehan, 1965 ; Breslow, 1970), le test de TaroneWare (1977), le test de Peto-Peto-Prentice (Peto et Peto, 1972 ; Prentice, 1978), et répond à une problématique identique : la comparaison des fonctions de survie, mais ils s’appuient sur des mécanismes différents. – Le test du « Log-Rank » Le test du Log-Rank est le test standard et le plus souvent utilisé parmi les tests de comparaison des courbes de survie. Pour tester l’égalité des fonctions de survie de deux ou plusieurs groupes, on doit comparer le nombre d’évènements (nombre de cessation d’activité des entreprises) observés dans chaque groupe au nombre d’évènements attendus. Pour cela, supposons que pour les 𝑟 groupes réunis, il y a 𝑘 temps d’évènements (d’échec) observés, ordonnés et distincts, 𝑡1 < 𝑡2 < ⋯ < 𝑡𝑘. On définit alors : – 𝑑𝑟𝑖 : le nombre total d’évènements observés (entreprises échouées) au temps 𝑡𝑖 dans chaque groupe. – 𝑛𝑟𝑖 : le nombre total des entreprises à risque au temps 𝑡𝑖 dans chaque groupe. La statistique du test du Log-Rank est calculée, comme indiqué ci-dessous au tableau 6.1. en construisant à chaque temps 𝑡𝑖 , 𝑟 × 2 tableaux de contingence. le test de Fleming-Harrington (Harrington et Fleming, 1982). L’ensemble de ces tests 

– Le test de « Wilcoxon » Le test de Wilcoxon (appelé aussi test de Gehen ou test de Breslow) est aussi un test de rang, et est construit de la même manière que le test du log-rank, sauf que le test de Log-rank est fondé sur une statistique qui donne des poids égaux à toutes les observations (𝑤𝑖 = 1), alors que le test de Wilcoxon donne plus de poids aux décès précoces, qu’aux décès tardifs dans la comparaison (Alberti et al., 2005). 6.1.2. Résultats de l’estimation non-paramétrique Dans cette section, nous allons seulement présenter les représentations graphiques des fonctions de survie des sous-populations de notre échantillon qui sont statistiquement hétérogènes, ainsi que les résultats des tests d’égalité des fonctions de survie, selon les différentes variables retenues (le genre, la période séparant le diplôme et la date de la création, l’occupation de l’entrepreneur préalable à la création, la motivation, le capital de démarrage, et la localisation géographique) . Les autres estimations des fonctions de survie menées sous l’hypothèse d’une population homogène, sont illustrées dans l’annexe 10.