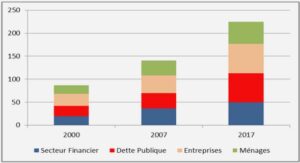
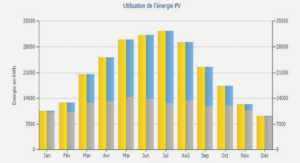
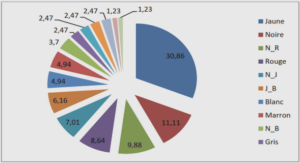
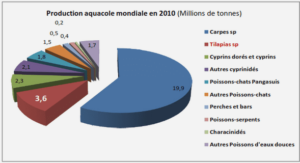
Mesure et gestion des risques en finance

Calculs de Malliavin pour les Processus des Sauts

Le calcul de Malliavin est un calcul différentiel infini-dimensionnel (calcul différentiel mais sur un espace de dimension infinie) ou, en d’autres termes, un calcul des variations stochastique. Le calcul de Malliavin suscite beaucoup d’intérˆet depuis quelques années, et les premiers travaux remontent a l’année 1976, par Paul Malliavin, qui a publié ”Stochastic calculus of variations and hypoelliptic operators”. Parmi les raisons de l’intérˆet pour le calcul de Malliavin, la portée des applications en mathématiques financiér`es, particuli`erement aux mod`eles basés sur le mouvement brownien. Mais des données empiriques ont montré les limites des mod`eles financiers browniens, cela a suscité un regain d’intérˆet pour les processus avec saut, par exemple le processus de Lévy, qui a un essor important dans les mod`eles du portefeuille d’une compagnie d’assurances, voir [37]. Pour cela, dans ce chapitre on explique les techniques des calculs de Malliavin pour les processus avec sauts, plus particuli`erement pour les processus de Lévy de saut pur. Pour plus de détails voir [20],[21], [31],[34] et [39].

Processus de Lévy de saut pur

Soit (Ω, F, P) l’espace de probabilité, et X = (Xt ;t ≥ 0) un processus de Lévy a valeurs à R d . Pour simplifier, dans ce chapitre on prendre d = 1, et de mˆeme pour B, B0, Θ, Θ∞,0 et ΘT,0. On définit la mesure de saut compensé N˜ associée au processus de Lévy X = {Xt , t ≥ 0}, qu’on appelle aussi mesure aléatoire de Poisson compensée : 2.1 Processus de Lévy de saut pur 24 N˜ (dt, dz) := N (dt, dz) − ν (dz) dt o`u ν = ν (dz), z ∈ R0, est une mesure de Lévy B0 et N la mesure aléatoire de Poisson associée au processus de Lévy X = {Xt , t ≥ 0}. Théor`eme 2.1.1 La décomposition de Lévy-Itˆo Soit X un processus de Lévy. Alors pour un processus standard de Wiener (mouvement brownien) W = W (t) t>0 (W (0) = 0), X = (Xt ;t ≥ 0) admet la représentation intégrale suivante : X (t) = αt + σW (t) + Z t 0 Z |z|<1 zN˜ (ds, dz) + Z t 0 Z |z|≥1 zN (ds, dz) (2.1) pour certaines constantes α, σ ∈ R. Voir [20] ou [39]. En particulier, on peut voir que si le processus de Lévy a des trajectoires continues alors il est de la forme X (t) = αt + σW (t), t ≥ 0. On peut prouver que si E [|X (t)| p ] < ∞, pour certains p ≥ 1, alors Z |z|≥1 |z| p ν (dz) < ∞, voir [39]. En particulier, si on suppose que E  X 2 (t)  < ∞, t ≥ 0, alors on a Z |z|≥1 |z| 2 ν (dz) < ∞, et la représentation (2.1) apparaˆıt comme X (t) = at + σW (t) + Z t 0 Z R0 zN˜ (ds, dz), (2.2) 2.2 Extension Chaotiques de Wiener – Itˆo 25 o`u a = α + R |z|≥1 zv (dz). On appelle processus de Lévy de saut pur, le processus de Lévy du type ci-dessus avec σ = 0.

Extension Chaotiques de Wiener – Itˆo

Dans cette section, on explique qu’il est possible d’obtenir une extension du chaos aux processus de Lévy à saut pur X = (Xt ;t ≥ 0), o`u a = σ = 0 en (2.2), voir [20], [31] et [34]. Cependant, dans ce cas, les intégrales itérées correspondantes doivent ˆetre prises par rapport à la mesure de Poisson compensée , associée à X : X (t) = Z t 0 Z R0 zN˜ (dt, dz) et non par rapport à X lui-mˆeme. 2.2.1 Intégrales Itérées de Itˆo Soit L 2 ((η × ν) n ) = L 2 (([0, T] × R0) n ) l’espace des fonctions f réelles déterministes telles que : ||f||L2((η×ν) n ) = Z ([0,T]×R0) n f 2 (θ1…, θn) dt1ν (dz1)…dtnν (dzn) 1 2 < ∞ o`u η(dt) = dt désigne la mesure de Lebesgue sur [0, T]. La symétrisation ˜f de f est défini par ˜f (θ1, …, θn) = 1 n! X σ f (tσ1 , zσ1, …, tσn , zσn ), o`u la symétrisation est sur les n paires θ1 = (t1, z1,), …, θn = (tn, zn) et non sur les 2n variables t1, z1, …, tn, zn, et la somme étant prise sur toutes les permutations σ = (σ1, σ2, …, σn) de {1, 2, …, n}. Une fonction f ∈ L 2 ((η × ν) n ) est appelée symétrique si f = ˜f. On note l’espace de toutes les fonctions symétriques dans L 2 ((η × ν) n ) par L˜2 ((η × ν) n ). On définit Gn := {(θ1, …, θn) : 0 ≤ t1 ≤ … ≤ tn ≤ T, zi ∈ R0, i = 1, …, n} et L 2 (Gn), l’ensemble des fonctions réelles g sur Gn , telles que 2.2 Extension Chaotiques de Wiener – Itˆo 26 ||g||L2(Gn) := Z Gn g 2 (θ1, …, θn) dt1ν (dz1)…dtnν (dzn) 1 2 < ∞ pour f ∈ L˜2 ((η × ν) n ). On a f11Gn ∈ L 2 (Gn), voir [20], et ||f||L2((η×ν) n ) = n! ||f||L2(Gn) . Définition 2.2.1 L’intégrale itérée de n fois Jn (g) pour tout g ∈ L 2 (Gn) est la variable aléatoire dans L 2 (P) (l’espace des variables aléatoires carrés intégrables) définie comme suit : Jn (g) := Z T 0 Z R0 … Z t − 2 0 Z R0 g (θ1, …, θn) N˜ (dθ1)…N˜ (dθn). En particulier on pose J0 (g) = g pour tout g ∈ R. Si f ∈ L˜2 ((η × ν) n ), on défini aussi In (f) := Z ([0,T]×R) n f (θ1, …, θn) N˜ ⊗n (dθ) := n!Jn (g) o`u N˜ ⊗n (dθ) = N˜ ⊗n (dt, dz) = N˜ (dt1, dz1)· · · N˜ (dtn, dzn). On appelle aussi In (f) l’intégrale itérée de n fois de f. Pour tout f ∈ L˜2 ((η × ν) n ) et g ∈ L˜2 ((η × ν) m ), on a les relations suivantes : E [Im (g) In (f)] =  0, n 6= m (g, f)L2((η×ν) n ) , n = m (n, m = 1, 2, …), (2.3) o`u (g, f)L2((η×v) n ) := Z ([0,T]×R0) n g (θ1, …, θn) f (θ1, …, θn) dt1ν (dz1)…dtnν (dzn). Pour plus de détails voir [20].

L’extension du Chaos de Wiener – Itˆo

Dans cette sous section, on peut maintenant formuler l’extension du chaos par rapport à la mesure aléatoire de Poisson associée au processus de Lévy X = {Xt , t ≥ 0}. Voir [20], [31].

Extension du chaos de Wiener –

Ito pour les mesures aléatoires de Poisson. Soit F ∈ L 2 (P) une variable aléatoire FT−mesurable. Alors F admet la représentation F = X∞ n=0 In (fn) avec une séquence unique d’éléments fn ∈ L˜2 ((η × ν) n ), n = 1, 2, …. Ici, on définit I0 (f0) := f0 pour les valeurs constantes f0 ∈ R. De plus, on a ||F||2 L2(P) = X∞ n=0 n! ||f||2 L2((η×ν)n) . (2.4) Preuve Par le théor`eme 9.10 de représentation d’Itˆo dans [20], il existe un processus prévisible ψ1 (θ1), θ1 ∈ ΘT,0 tel que F = E [F] + Z ΘT ,0 ψ1 (θ1) N˜ (dθ1), o`u ||F||2 L2(P) = (E [F])2 + E « Z ΘT ,0 ψ 2 1 (θ1) dt1ν (dz1) # < ∞. Par conséquent pour presque tout θ1 ∈ ΘT,0, il existe un processus prévisible ψ2 (θ1, θ2), (θ2) ∈ Θt1,0, tel que ψ (θ1) = E [ψ (θ1)] + Z ΘT ,0 ψ2 (θ1, θ2) N˜ (θ2). Cela donne F = E [F] + Z ΘT ,0 ψ1 (θ1) N˜ (dθ1) + Z T 0 Z R0 Z t − 1 0 Z R0 ψ2 (θ1, θ2) N˜ (dθ2) N˜ (dθ1). On définit g0 := E [F] et g1 (θ1) := E [ψ1 (θ1)] , θ1 ∈ ΘT,0 On fait la mˆeme chose pour θ2, cela donne 2.3 Opérateurs de Malliavin et Skorohod 28 F = X k−1 n=0 J (gn) + Z GK Z R0 ψk (θ1, …, θk) N˜ ⊗k (dθ). En procédant comme dans la démonstration du théor`eme 1.10 dans [20] , on peut voir que le terme résiduel ci-dessus s’annule, c’est-à-dire Z R0 ψkN˜ ⊗k (dθ) → 0, k → ∞, Avec la convergence en L 2 (P). Cela donne l’extension du chaos F = X∞ n=0 Jn (gn). dans L 2 (P) avec gn ∈ L 2 (P), n = 1, 2, …. On étend la fonction gn sur l’ensemble ([0, T] × R0) n en mettant gn := 0 sur ([0, T] × R0) n \ Gn et défini par fn := ˜gn, alors In (fn) = n!Jn (fn) = n!Jn (˜gn) = Jn (gn) Ainsi on obtient F = X∞ n=0 In (fn). De plus, l’isométrie de la formule (2.4) est obtenue directement à partir de (2.3).  2.3 Opérateurs de Malliavin et Skorohod 2.3.1 L’intégrale de Skorohod Définition 2.3.1 Soit X = {X (θ), θ ∈ ΘT,0} un processus stochastique tel que X (θ) est une variable aléatoire FT−mesurable pour tout θ ∈ ΘT,0 et E [X2 (θ)] < ∞. Alors pour chaque θ ∈ ΘT,0 on a la décomposition en chaos X (θ) = X∞ n=0 In (fn (., θ)) o`u fn (., θ) ∈ L˜2 ((η × ν) n ) 2.3 Opérateurs de Malliavin et Skorohod 29 Soit ˜fn (θ1, …, θn, θn+1) la symétrisation de fn (θ1, …, θn, θ) en fonction des n + 1 paires θ1, …, θn, θ = θn+1,et tel que X∞ n=0 (n + 1)!       ˜fn       2 L2((η×ν)n+1) < ∞. On définit alors l’intégrale de Skorohod δ (X) de X par rapport à N˜, avec X ∈ Dom (δ) par : δ (X) = Z ΘT ,0 X (θ) N˜ (δt, dz) := X∞ n=0 In+1  ˜fn  . pour plus de détails, voir [20], [21], [28] et [29]. Théor`eme 2.3.1 L’intégrale de Skorohod comme extension de l’Intégral d’Itˆo 1. Soit X = {X (θ), θ ∈ ΘT,0} un processus prévisible tel que E Z T 0 Z R0 X 2 (θ) ν (dz) dt < ∞. Alors X est à la fois, au sens d’Itˆo et de Skorohod, intégrable par rapport à N˜ et Z ΘT ,0 X (θ) N˜ (dθ) = Z ΘT ,0 X (θ) N˜ (δt, dz). 2. Soit Y = Y (t), t ∈ [0, T] , un processus prévisible tel que E Z T 0 Y 2 (t) dt < ∞ Alors Y est à la fois d’Itˆo et de Skorohod, elle est intégrable par rapport à X et Z ΘT ,0 Y (t) δX (dt) = Z ΘT ,0 Y (t) dX (t). Voir [20] pour plus de détails sur ce Théor`eme. 2.3.2 La Dérivée de Malliavin Définition 2.3.2 Soit D1,2 l’espace stochastique de Sobolev constitué de toutes les variables aléatoires mesurables F ∈ L 2 (P) avec la décomposition en chaos 2.3 Opérateurs de Malliavin et Skorohod 30 F = X∞ n=0 In (fn), fn ∈ L˜2 ((η × ν) n ), satisfaisant le crit`ere de convergence ||F||2 D1,2 = X∞ n=1 nn! ||fn||2 L2((η×ν)n) < ∞. En comparant la condition sus-mentionnée dans (2.4), on voit que D1,2 est strictement contenu dans l’espace de toutes les variables aléatoires FT−mesurable dans L 2 (P), voir [20], [21] et [34] . Définition 2.3.3 On définit l’opérateur D : Dθ : F ∈ D1,2 ⊂ L 2 (P) −→ DF ∈ L 2 (η × ν × P) par DθF = X∞ n=1 nIn−1 (fn (., θ)), θ ∈ ΘT,0 avec In−1 (fn (·, θ)) que c’est que l’intégrale itérée (n − 1) de fn. On appelle DθF la dérivé de Malliavin de F en θ, voir [20], [21]. Exemple 2.3.1 Si F = R ΘT ,0 f (θ) N˜ (dθ), et si la fonction f ∈ L 2 (η × ν) c’est deterministe, alors F = I1 (f) et DθF = I0 (f1 (·, θ)) = f (θ). En particulier, si F = X (t) := R ΘT ,0 zN˜ (dθ), alors DθF = z. Théor`eme 2.3.2 Formule de dualité Soit X(θ) = X(t, z), t ∈ R+, z ∈ R un processus intégrable de Skorohod et F ∈ D1,2. Alors la relation de dualité est E [δ (X) F] = Z T 0 Z R X (θ) DθF ν (dz) dt Preuve Pour la démonstration de ce théor`eme voir [10], [18], [20], [34], et [36]. 2.3 Opérateurs de Malliavin et Skorohod 31 Théor`eme 2.3.3 Intégration par parties Soit X(θ) = X(t, z), t ∈ R+, z ∈ R un processus stochastique intégrable au sens de Skorohod et F ∈ D1,2 tel que le produit X(θ)·(F +D∞F) est intégrable au sens de Skorohod. Alors F Z T 0 Z R X (θ) N˜ (δt, dz) = Z T 0 Z R X (θ) (F + DθF)N˜ (δt, dz) + Z T 0 Z R X (θ) DθF ν (dz) dt. Preuve Soit D ε 1,2 l’ensemble des combinaisons linéaires d’exponentielles, on suppose d’abord que F ∈ D ε 1,2 , et G ∈ D ε 1,2 . Alors, on obtient par le théor`eme 2.3.2 et le théor`eme 12.7 de [20] : E  G Z ∞ 0 Z R F X (θ) N˜ (δt, dz)  = E Z ∞ 0 Z R F X (θ) DθGv (dz) dt = E  GF Z ∞ 0 Z R X (θ) N˜ (δt, dz)  − E  G Z ∞ 0 Z R X (θ) DθF ν (dz) dt − E  G Z ∞ 0 Z R X (θ) DθFN˜ (δt, dz)  = E  G  F Z ∞ 0 Z R X (θ) N˜ (δt, dz) − Z ∞ 0 Z R X (θ) DθF v (dz) dt − Z ∞ 0 Z R X (θ) DθFN˜ (δt, dz)  . La preuve suit alors par un argument de densité appliqué à F et G.