La méthode PERT permet d’ évaluer la durée de réalisation d’un projet complexe et de détecter les parties de ce projet ne supportant aucun retard. Elle résout des problèmes appelés problèmes d’ordonnancement. Le projet sera subdivisé en tâches. En général, elles ne pourront toutes être réalisées simultanément, certaines tâches devront être achevées avant que d’autres ne puissent débuter. On résumera l’information sur le projet sous la forme d’un tableau, appelé échéancier, où seront indiquées les tâches, leur durée, et les contraintes d’antériorité à respecter.
Construction du graphe PERT
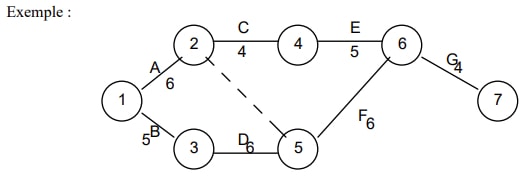
La méthode commence par la construction d’un graphe, appelé graphe PERT, à partir de l’échéancier. Ce graphe sera un graphe valué dont les arcs seront les tâches, les valeurs des arcs étant leur durée et les sommets représenteront des états d’avancement du projet, numérotés de 1 à n. Le graphe devra respecter deux contraintes : a) en un sommet, toutes les tâches se trouvant sur un chemin y menant, doivent être achevées b) il n’y a pas d’arc de i vers j avec i est supérieur à j On a été obligé d’ajouter un arc allant de 2 à 5 pour tenir compte du fait que A devait être terminée pour que F commence, cette tâche sera appelée tâche fictive et sera de durée nulle. Pour construire un graphe PERT dans le cas général, on procèdera de la manière suivante..
Détermination des niveaux des tâches
On attribuera le niveau 0 aux tâches qui n’ont pas de tâche antérieure. On attribuera le niveau 1 aux tâches dont les tâches antérieures sont de niveau 0. On déterminera ainsi le niveau de chaque tâche : les tâches de niveau k+1 seront les tâches dont les tâches antérieures sont de niveau inférieur avec au moins une tâche de niveau k parmi elles. On construira le graphe en traçant les tâches par ordre de niveau croissant.
Tâches commençantes, finissantes, convergentes
Avant de se lancer dans la construction du graphe, il sera souvent utile de détecter les tâches dites commençantes, finissantes ou convergentes. Les tâches commençantes sont les tâches sans tâche antérieure, elles partent du sommet 1 du graphe (appelé entrée du graphe). Les tâches finissantes sont les tâches qui ne sont pas tâche antérieure, elles arrivent au sommet terminal du graphe (appelé sortie). Les tâches convergentes sont des tâches que l’on rencontre toujours ensemble (i.e. jamais l’une sans l’autre) dans la colonne « tâches antérieures »; dans le graphe, elles auront le même sommet terminal.
Détermination des dates et des marges
Une fois le graphe construit, on va déterminer les dates au plus tôt et au plus tard pour les différents sommets et les marges libres et totales pour les tâches.
Dates au plus tôt
Pour un sommet, la date au plus tôt (notée : t) représente concrètement le temps minimum nécessaire pour atteindre ce sommet ( on ne peut pas faire mieux). Elle se déterminera de proche en proche, par ordre de sommet croissant, à partir de l’entrée du graphe, grace à l’algorithme de Ford de recherche du chemin le plus long. Ainsi :
t1 = 0 et tj = Max ( ti + dij ) sur tous les i précédant j avec dij = durée de la tâche ij
Dans l’exemple, t1 = 0, t2 = 0+6 = 6, t3 = 0+5 = 5, t4 = 6+4 = 10, t5 = max ( 6+0 , 5+6 ) = 11, t6 = max ( 11+6 , 10+5 ) = 17, t7 = 17+4 = 21.
La date au plus tôt de la sortie du graphe représente la durée minimale réalisable pour l’ensemble du projet ( dans l’exemple, t7 = 21, le projet durera donc au mieux 21 jours)
Dates au plus tard
Pour un sommet, la date au plus tard (notée : T ) représente concrètement la date à laquelle cet état doit obligatoirement être atteint si l’on ne veut pas augmenter la durée totale du projet ( il ne faut pas faire pire ). Elle se déterminera de manière analogue à t, mais par ordre de sommet décroissant, depuis la sortie du graphe :
Tn = tn = Durée du projet et Ti = Min ( Tj – dij ) sur tous les j suivant i Dans l’exemple, T7 = 21, T6 = 21 – 4 = 17, T5 = 17 – 6 = 11, T4 = 17 – 5 = 12, T3 = 11 – 6 = 5, T2 = min ( 11-0 , 12-4 ) = 8, T1 = min ( 8-6 , 5-5 ) = 0 On aura toujours t1 = T1 = 0 et t inférieur ou égal à T pour tout sommet. On appelle T-t la marge de flottement du sommet.
Marges des tâches
La marge libre d’une tâche représentera concrètement le retard maximal qu’ on pourra prendre dans la réalisation d’une tâche sans retarder le début des tâches suivantes, on la notera ML.
La marge totale d’une tâche représentera concrètement le retard maximal qu’ on pourra prendre dans la réalisation d’une tâche sans retarder l’ensemble du projet, on la notera MT.
Si on note ij la tâche allant du sommet i au sommet j : MLij = tj – ti – dij et MTij = Tj – ti – dij
Compte tenu du mode calcul, les marges seront toujours positives ou nulles et la marge libre d’une tâche sera toujours inférieure ou égale à sa marge totale. On qualifiera de critique, une tâche dont la marge totale est nulle, c’est en quelque sorte une tâche « urgente », une tâche sur laquelle il ne faut pas prendre de retard si l’on ne veut pas augmenter la durée totale du projet. Si la durée d’une tâche augmente, une partie de cette augmentation sera absorbée par la marge de la tâche, seul le sur plus se répercutera sur la durée du projet.






