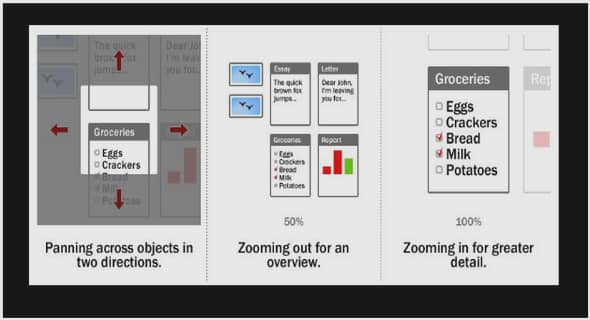
Le modèle physique

Le modèle physique ainsi que l’approche de modélisation dite darcéenne multidomaine sont présentés dans cette partie. La modélisation des écoulements souterrains et de subsurface est d’abord abordée. La modélisation des processus de surface, l’approche globale et la modélisation du phénomène de transport sont ensuite détaillées. Nous rap- pelons ici que notre modèle s’inscrit dans le formalisme défini par Freeze et Harlan [Freeze et Harlan, 1969]. La modélisation des écoulements de subsurface est relativement classique et ne sera pas présentée en détails. En revanche, le développement de l’équation décrivant les écoulements de surface sera décrit complètement même si certaines équations ont déjà été présentées dans la partie précédente. Comme décrit dans la partie précédente, on utilise les équations résultant de la combinaison de l’équation de conservation de la masse et des équations de Darcy et Richards pour décrire les écoulements dans les zones saturée et non saturée :avec t le temps [T ], H = h+z la charge hydraulique [L], h étant la pression d’eau exprimée en mètre [L] et z la côte du point considéré [L], S le coefficient d’emagasinement [L¡1], C(h)= @µ/@h la capacité capillaire [L¡1], µ étant la teneur en eau, Ksat la conductivité hydraulique à saturation, K(h) la conductivité hydraulique du milieu dans la zone non saturée [LT ¡1] et q le terme source/puits d’eau [T ¡1]. De façon courante, on écrit dans le domaine non saturé : K(h) = Ksat £ kr(h) avec kr(h) la perméabilité relative du milieu considéré.

Les équations 1.1 peuvent également être écrites en fonction de la teneur en eau µ. On préférera cependant l’écriture en fonction de la pression h car elle permet de modéliser les écoulements dans la zone saturée et la zone non saturée dans un seul domaine de calcul. Ce point est particulièrement important dans notre approche de modélisation et est une des particularités du code de calcul utilisé, Cast3m. Pour cela, on définit les fonctions caractéristiques de teneur en eau µuni(h), de capacité capillaire Cuni(h) et de conductivité hydraulique Kuni(h) unifiées dans l’ensemble des gammes de pressions de la manière suivante (cf figure 1.1) : L’utilisation de l’équation 1.5 pour modéliser les écoulements dans la zone non saturée nécessite la connaissance des lois caractéristiques des sols. Ces courbes peuvent avoir une grande influence sur la dynamique de la zone non saturée (e.g. [Vogel et al, 2001]). On choisit pour l’ensemble des cas présentés dans la suite de ce manuscrit les équations de Van Genuchten [Van Genuchten, 1980] pour la teneur en eau et la perméabilité relative. L’emploi de ces équations est très classique. La teneur en eau µ(h) et la perméabilité relative kr(h) dans le formalisme de Van Genuchten peuvent s’écrire :Dans notre modèle, des conditions aux limites de Neuman (condition de flux imposé) ou de Dirichlet (condition de charge imposée) peuvent être imposées aux frontières du domaine de calcul.

Les écoulements de surface

L’équation de conservation de la masse pour les écoulement de surface peut s’écrire de la manière suivante [Beven, 2001] :de lame d’eau moyennée hs [Kirkby, 1978]. L’équation de Manning-Strickler a été choisie pour décrire cette relation dans nos travaux. On suppose alors que les écoulements en surface se produisent dans un film d’eau de faible épaisseur et que cette épaisseur peut être négligée devant l’étendue latérale de la lame d’eau. La relation de Manning est très souvent utilisée pour modéliser les écoulements de surface et peut s’écrire de la manière suivante [Beven, 2001] :où Us;i est la norme de la vitesse dans la direction i (direction x ou y), n [LT ¡1=3] est le paramètre de Manning-Strickler caractérisant la rugosité du sol et Sf;i la pente dite de friction dans cette même direction. L’étape suivante consiste à réécrire cette équation de la manière suivante :Dans le cadre de l’approximation de l’onde diffusive, on suppose que le gradient de hauteur de lame d’eau est faible devant la pente topographique du sol et que la pente de friction peut être approximée par la pente de la lame d’eau. On obtient alors [Wasantha, 1998b] :Cette équation a la même forme mathématique que l’équation de diffusivité permettantde décrire les écoulements dans la zone saturée et la zone non saturée (Eq ??). Ce constat est le fondement de notre approche de modélisation. La forme de l’équation 1.15 nous laisse penser que l’on peut modéliser les écoulements de surface comme des écoulements dans un milieu poreux aux propriétés particulières. On introduit donc à la surface de notre domaine de calcul une couche de milieu poreux, appelée couche de ruissellement, qui nous permettra de représenter les processus de surface (voir Fig 1.2). On crée ainsi un continuum de milieux darcéens couvrant l’intégralité des domaines de surface et de subsurface et permettant de modéliser de façon intégrée les processus de surface et de subsurface et leurs interactions. Les prochains paragraphes détaillent la définition des fonctions caractéristiques de conductivité hydraulique et de teneur en eau de ce milieu poreux particulier.