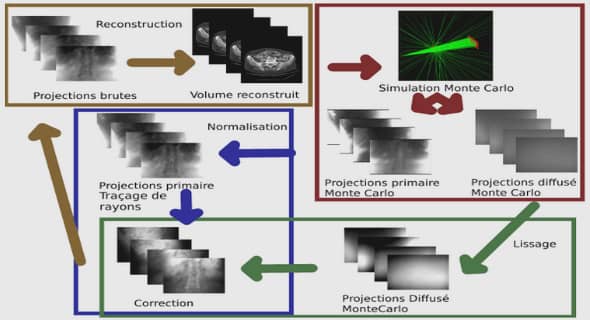
Le monoïde de Baxter

Il existe une large gamme de monoïdes définis en tant que quotients du monoïde libre et dont les classes d’équivalence sont indexées par des objets combinatoires. Le premier exemple histo- rique et sans doute le plus fondamental, est le monoïde plaxique [LS81], [Lot02]. Une définition de ce monoïde repose sur la donnée d’une congruence sur les mots obtenue à partir des relations de Knuth [Knu70]. Une autre approche, plus algorithmique, consiste à partir de l’algorithme de Schensted [Sch61], qui permet de déterminer sur l’entrée d’un mot, la longueur de son plus long sous-mot croissant. Cet algorithme construit un effet un tableau de Young à partir d’un mot, et il est naturel de considérer que deux mots sont équivalents s’ils produisent le même tableau lorsqu’on les insère. Il s’avère que ces deux approches mènent à la construction du même mo- noïde, que les éléments de ce dernier peuvent s’interpréter comme des tableaux de Young et que le produit du monoïde se calcule par l’intermédiaire de l’algorithme de Schensted. La principale illustration de l’importance du monoïde plaxique est son intervention dans la démonstration de la règle de Littlewood-Richardson [LR34] pour calculer les coefficients qui apparaissent lors de la multiplication de deux fonctions de Schur [Mac95]. Il permet de plus de construire une généralisation de l’algèbre des fonctions symétriques [Mac95] en la plongeant dans l’algèbre des tableaux de Young, rendant plus limpides certaines propriétés des fonctions symétriques.

Plus récemment, d’autres monoïdes qui ont des caractéristiques semblables au monoïde plaxique ont été introduits et étudiés. L’exemple le plus convaincant est dans doute le monoïde sylvestre [HNT02], [HNT05], qui, tout comme le monoïde plaxique, peut être défini de deux manières équivalentes, soit par une congruence sur les mots, soit par un algorithme d’insertion. Dans ce cas, c’est l’algorithme d’insertion dans un arbre binaire de recherche [AU94], [Knu98], [CLRS03] qui joue le rôle de l’algorithme de Schensted, et les objets du monoïde sont des arbres binaires de recherche. De plus, tout comme dans le cas plaxique, le monoïde sylvestre est un tremplin pour la construction d’une algèbre qui généralise celle des fonctions symétriques [LR98], [HNT05]. Notons que sous certaines conditions, de tels monoïdes mènent à la construction de treillis. Par exemple, le monoïde sylvestre offre une construction très intéressante [HNT05] du treillis de Tamari [Tam62], [HT72].L’objectif de ce chapitre est d’introduire et d’étudier un monoïde semblable au monoïde plaxique et au monoïde sylvestre, dont les classes d’équivalence sont en bijection avec les objets de la famille combinatoire de Baxter. La famille combinatoire de Baxter est constituée des classes combinatoires en bijection avec les permutations de Baxter [Bax64], qui sont des permutations qui évitent certains motifs. Citons par exemple les couples d’arbres binaires jumeaux [DG94], les quadrangulations [ABP04] et les orientations planes bipolaires [BBMF08], qui sont des objets de cette famille. Nous considérerons spécialement les couples d’arbres binaires jumeaux comme représentants de cette famille.

Ce chapitre est organisé comme suit. Dans le paragraphe 4.1, nous présentons les concepts de base sur les monoïdes semblables au monoïde plaxique. Nous passons ensuite en revue quelques exemples de tels monoïdes : le monoïde plaxique, le monoïde sylvestre, le monoïde de Bell, et enfin, le monoïde des k-reculs. La définition du monoïde de Baxter est donnée dans le para- graphe 4.2. Nous y dégageons ses premières propriétés, ainsi que les liens qu’il entretient avec certains des monoïdes sus-cités. Le paragraphe 4.3 est consacrée à construire un analogue de l’algorithme d’insertion et de la correspondance de Robinson-Schensted. Nous associons ainsi bijectivement à tout mot, un couple de couples d’arbres binaires jumeaux étiquetés soumis à certaines conditions. Cette correspondance fait intervenir deux algorithmes d’insertion dans un arbre binaire de recherche, ainsi que la combinatoire des arbres binaires croissants et dé- croissants. De plus, à partir d’un couple d’arbres binaires jumeaux étiqueté J, nous proposons divers algorithmes d’extraction pour calculer un mot particulier dans la classe encodée par J. Nous terminons par le paragraphe 4.4 en rappelant la construction qui à une congruence d’un treillis associe un treillis quotient. La congruence de Baxter est, comme nous le montrons, une congruence du permutoèdre. Étant donné que les classes d’équivalence de permutations sous la congruence de Baxter sont en bijection avec les couples d’arbres binaires jumeaux non étiquetés, la congruence de Baxter définit un treillis quotient du permutoèdre sur l’ensemble de ces élé- ments. Nous décrivons ses relations de couverture et montrons que ce treillis est très similaire au treillis de Tamari. Un nouvel objet de la famille combinatoire de Baxter est finalement introduit, à savoir les diagrammes de Tamari doubles, dans le but de pouvoir comparer facilement deux éléments dans ce treillis.