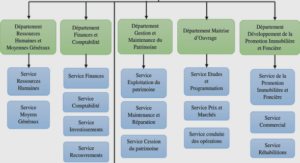
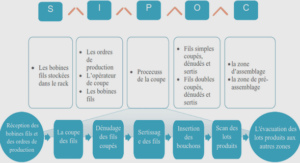
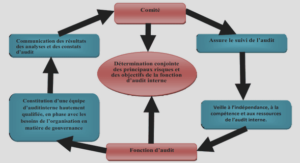
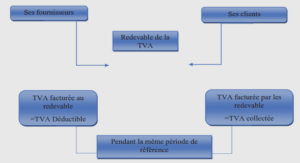
L’algèbre de Hopf des couples.

Dans ces dernières années, un grand nombre d’algèbres de Hopf combinatoires dont les bases sont indexées par divers objets combinatoires plus ou moins exotiques ont été activement étu- diées. Par exemple, l’algèbre de Hopf des permutations, initialement définie par Malvenuto et Reutenauer [MR95] et appelée algèbre de Hopf de fonctions quasi-symétriques libres ou en- core FQSym, a donné lieu à de nombreuses publications [Mal93], [DHT02], [LR02], [AS05], [DHNT08] (voir aussi le paragraphe 2.2.3 du chapitre 2 où l’on rappelle la définition de cette algèbre de Hopf et quelques-unes de ses propriétés que nous utiliserons dans la suite). Celle-ci est intéressante à bien des points de vue et notamment parce qu’elle admet un grand nombre de sous-algèbres de Hopf. Citons par exemple l’algèbre de Hopf FSym des fonctions symétriques libres [PR95], [DHT02] basée sur les tableaux de Young standard, l’algèbre de Hopf Bell [Rey07] basée sur les partitions d’ensemble, l’algèbre de Hopf PBT de Loday-Ronco [LR98], [HNT05] basée sur les arbres binaires, ainsi que l’algèbre de Hopf Sym des fonctions symétriques non commutatives [GKL95] basée sur les compositions d’entiers. Une approche unificatrice pour construire toutes ces structures débute par la définition d’un bon monoïde (voir la définition 4.1.4 du chapitre 4). En effet, FSym s’obtient directement à partir du monoïde plaxique [LS81], Bell à partir du monoïde de Bell [Rey07], PBT à partir du monoïde sylvestre [HNT02], [HNT05] et Sym à partir du monoïde hypoplaxique [KT97], [Nov98]. La richesse de cette approche tient au fait que, en plus d’obtenir des algèbres de Hopf, cette construction apporte au passage la plupart du temps des posets, des algorithmes combinatoires et des analogues d’algorithmes d’insertion et de correspondance de Robinson-Schensted, d’intérêts propres.

L’objectif premier de ce chapitre est d’enrichir cette collection de sous-algèbres de Hopf de FQSym par l’introduction d’une algèbre de Hopf basée sur les couples d’arbres binaires jumeaux (voir la définition 4.2.1 du chapitre 4). Pour ce faire, nous décrivons en détail le procédé de construction formalisé par Hivert et Nzeutchap [HN07] qui, à un bon monoïde, associe une sous-algèbre de Hopf de FQSym. Nous présentons, en tant que résultats intermédiaires, des propriétés générales des algèbres de Hopf ainsi construites. L’algèbre de Hopf que nous obtenons découle de la définition du monoïde de Baxter (dont l’introduction et l’étude figurent dans le chapitre 4) et est étudiée sous la loupe des propriétés que nous avons dégagées.Dans le but d’illustrer par des exemples les relations existantes entre les congruences de treillis (voir la définition 4.4.1 du chapitre 4) et les algèbres de Hopf, Reading présenta dans [Rea05] une congruence du permutoèdre dont les classes d’équivalence sont indexées par les permutations de Baxter tordues (la définition de ces permutations figure dans le paragraphe 4.3.3 du chapitre 4). Cette congruence est très naturelle : la borne inférieure de deux congruences du permutoèdreCe chapitre est organisé comme suit. Dans le paragraphe 5.1.1, nous rappelons la construction qui à un bon monoïde associe une sous-algèbre de Hopf de FQSym. Nous présentons aussi en guise d’exemples les constructions de FSym, PBT et Sym. Le paragraphe 5.2 recense des propriétés générales des algèbres de Hopf obtenues selon ce procédé. Nous montrons en particulier que lorsque la congruence utilisée pour définir un bon monoïde est aussi une congruence de treillis, le produit dans la base fondamentale de l’algèbre de Hopf associée s’exprime comme un intervalle du treillis quotient du permutoèdre. Nous proposons également dans ce cas des bases multiplicatives et montrons que la structure est libre en tant qu’algèbre. Nous introduisons ensuite le concept de base booléenne et donnons une condition nécessaire sur le bon monoïde pour que la base fondamentale de l’algèbre de Hopf associée en soit une. Nous rappelons enfin la notion de bigèbre bidendriforme due à Foissy [Foi07], [Foi09] et donnons une condition nécessaire pour que l’algèbre de Hopf construite admette une telle structure, impliquant entre autres son autodualité. Le paragraphe 5.3 est finalement consacrée à notre construction de l’algèbre des couples d’arbres binaires jumeaux ainsi qu’à son étude.

impliquées dans la construction de PBT peut être considérée comme l’un des points de départ dans la construction de Sym ; une question naturelle est donc de comprendre ce qu’il se passe lorsque c’est la borne supérieure qui est considérée. Reading montra que sa congruence du permu- toèdre est précisément cette dernière et que les plus petits éléments de ses classes d’équivalence sont des permutations de Baxter tordues. En outre, et grâce à sa théorie, il obtint gratuitement une algèbre de Hopf basée sur les permutations de Baxter tordues. En réalité, les permutations de Baxter et les permutations de Baxter tordues sont en bijection (voir le paragraphe 4.3.3 du chapitre 4). Law et Reading [LR10] mentionnèrent que la première démonstration de cette propriété fut apportée par West dans une note non publiée. Par conséquent, l’algèbre de Hopf de Reading définie en [Rea05] peut déjà être vue comme une algèbre de Hopf sur les couples d’arbres binaires jumeaux, et notre construction en est une différente d’une même algèbre de Hopf. De plus, Law et Reading [LR10] ont très récemment détaillé leur construction et étudié quelques-unes des propriétés de cette algèbre de Hopf. Si le point de vue de Law et de Reading mène comme le nôtre globalement aux mêmes résultats, notre cheminement est différent, ce qui offre différentes manières de comprendre cette construction, l’une centrée sur la théorie des treillis, l’autre axée sur la combinatoire des mots. De plus, une grande partie des résultats de ce chapitre ne se trouve pas dans [LR10], et réciproquement. Par exemple, dans notre cas, nous donnons une réalisation polynomiale de l’algèbre de Hopf des couples d’arbres binaires jumeaux, montrons qu’elle admet une structure de bigèbre bidendriforme, qu’elle est libre, autoduale et donnons deux bases multiplicatives.pour tout tableau de Young standard T . Cette réalisation polynomiale fournit l’une des dé- monstrations les plus limpides [Lot02] de la règle de Littlewood-Richardson [LR34] qui décrit un moyen de calculer le produit.