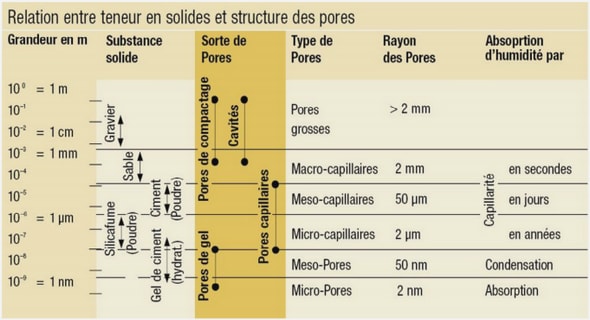
La modélisation des transferts d’air dans les bâtiments

La modélisation des transferts d’air dans les bâtiments

MOUVEMENTS D’AIR ENTRE ZONES

Les mouvements d’air dans un logement sont régis par les champs de pression régnant dans chaque volume du logement. L’emploi des hypothèses simples (et réalistes), vérifiées assez correctement par l’expérience, permet d’aborder avec une précision très raisonnable un problème initialement complexe. Pour simplifier, nous allons supposer que les températures d’air dans les volumes intérieurs et dans l’espace extérieur sont constantes dans l’espace et dans le temps. Il n’est pas indispensable de prendre cette hypothèse : une température stratifiée dans chaque volume peut être utilisée (voir annexe 1) mais le manque de connaissances actuelles sur ce phénomène et la complication qui en résulte, nous oblige â remettre la prise en compte de la stratification â une phase ultérieure (64). Puisque les températures sont constantes, il n’y a pas de bilan thermique à faire a priori. Par contre, il y a des échanges d’air, phénomène physique causé, d’une part, par la différence des masses volumiques de l’air des différentes pièces et. d’autre part, par la dépression (supression) créée par le vent ou/et l’extracteur mécanique. 94 6.1 – MODELISATION Pour calculer les échanges aérauliques entre les différents volumes du bâtiment plusieurs approches sont possibles (9) [10) [74) [105). Nous avons choisi une modélisation dite « nodale » (ou multizone en pression). Cette méthode consiste à considérer chaque volume du logement comme le volume de conTrôle d’un sous ensemble du système complet du bâtiment et d’étudier ses interactions avec les autres zones en écrivant les équations de bilans de masse (voir figure 1). © © — H – 4= © — H – 4f © 4- – H — © 4 © © figure 1 : Exemple aun logement û Quatre zones et au schéma Oes interactions (flux a ait) entre eux et avec l’extérieur.

Equation d’état

En chaque point de la zone i (numéro de la zone). l’air est assimilé à un gaz parfait dont l’équation d’état est : ou ?; « i-rr ( « ) masse volumique de l’air de la zone I pression absolue de la zone i température de la zone i constante de l’air = 287 (kg/m3 ) (Pa) (K) (J/kg.K)

Equation d’éauilibre de l’olr Intérieur

On suppose que le champ de pression dans chaque zone est celui du champ « hydrostatique ». En effet, l’expérience a montré (47) (103) que dans presque TOUT le volume, sauf très près des ouvertures, les vitesses d’air sont très faibles et que le champ de pression est très voisin du champ statique (voir figure 2). d P i 11) avec : g : accélération de la pesqnteur = 9.81 (m/s2 ) z : niveau par rapport à un plan de référence (m) L’équation (2) s’intègre compte tenu de réqudtion (1) et de l’hypothèse sur le champ de température : log • p i(*n g .P¡(0)J » « T Cette expression est valable pour un champ de température « stratifié » comme on en trouve dans les volumes du bâtiment. ici on se contente de T, • C** d’où : Pi(z) * P¡(0) er T i M En se limitont à un développement au premier ordre (erreur de l’ordre de lO’^z2 ) on peut écrire : PiO 1 (5″) soit Pi(z) « Pa -p.gz 96 «••>/• . MWM ».S*V.*., ».*~ »t-.. -« .«L-——ir.-1 !.—• • IM T.mrn. Figure 2 – V/fesses oe loir mesurées dons une cellule expérimentale au CSTB avec un aéblt d’entrée a air Oe 30 m/h (103). 6.13 – Chomp de pression extérieur en présence du vent On va supposer que le modèle « hydrostatique » précédent reste valable et qu’on lui ajoute un effet de pression dynamique du vent sur les façades du logement et en particulier sur ses ouvertures. En un point M de la structure et à. l’instant t la pression du « node extérieur » sera dès lors : P. (M) = Prf + lpeUjCp(M) – pegz (é ) QÙ: U0 Cp : vitesse du vent en un point de référence du bâtiment (m/s) : coefficient de pression du vent mesuré en soufflerie C /. On rencontre ici une hypothèse couramment utilisée par la plupart des auteurs (39) (59) (128). Il est pourtant important de noter que cette hypothèse est discutable surtout lorsqu’on sait que les Cp mesurés le sont pour des parois pleines sans ouvertures donnant â l’extérieur (portes, fenêtres). Des expériences sont en cours au CSTB pour préciser les limites du domaine de validité de cette hypothèse.

La masse de l’air à l’Intérieur de choque zone

Par définition, pour chaque zone la masse de l’air intérieur peut s’écrire : Mj-p.V . (?) où V, est le volume (m3 ) de la zone i. On admettra que ceci reste vrai même quand la fluctuation de la pression modifie Cela revient â dire que compte tenu de ses dimensions, on considérera que la pression varie instantanément dans tout le volume (pas d’ondes de pression). A remarquer que ceci n’est valable que pour des temps caractéristiques de fluctuation grands vis-à-vis des temps de transit des ondes acoustiques dans le volume. Exemple : pour une dimension de pièce de 5 m. le temps « acoustique » est de l’ordre de 5/340 soit 1/70 seconde. En gros cela veut dire que le modèle ne tient que si les St considérés sont > 1/10 seconde et par conséquent, il est Inutile de regarder les « fréquences » de turbulence plus élevées que 10 HZ. 98 6.15 – Equations de bilan de zones Pour chaque zone i le bilan de masse de l’air peut s’écrire : – y – ï (mj^i – m^ ) (r ) où m\->\ ‘• masse d’air sortant de la zone i ( kg/s ) nij_>i : masse d’air entrant dans la zone i ( kg/s ) N : nombre de zones sou Q; = I (m^j – àj^j) Compte tenu de (?) et de l’hypothèse d' »homogénéité » instantanée de la pression on a : dp. ou encore compte tenu de (1) : rTj dt y i ^ avec P. = P¡0 – p. g z Or dans un volume d’une pièce, z varie de quelques mètres et J3 . environ 1.2 à 1.3 kg/m3 donc le terme Ç,gz peut valoir environ 1.3 x 10 x ¿z soit 130 Pa pour Az=10 m Par contre Pto est de l’ordre de grandeur de la pression atmosphérique (environ 105 Pa). 99 Si on néglige le terme C¡gz dans la valeur de Pr l’Incertitude relative sur la valeur de la pression est inférieure à 0.2 % d’où réduction (10) devient : ^ £ « Q. (M) rT= dt V | K Une autre méthode peut conduire au même résultat : en effet, si on remplace P, par sa valeur dans (10) on a : rT; dt rT, i dt » y» ou bien compte tenu de ( ) V: dP: JlïlL0 .(i + u)Q . «o (41) rT: dt ^ rT: ; V l K i » . Un raisonnement analogue à celui fait précédemment montre que gr/rT, < 10″3 et par conséquent on peut négliger ce terme devant l’unité, d’où l’on retrouve l’éauation (11 ). On peut aussi justifier ceci en constatant qu’on peut améliorer l’approximation en prenant pour z une valeur moyenne sur la hauteur de Id pièce et de ce fcit en posont : a = Î- S = ctt moy r j *- l’équation (U) devient Vi dPi r T i -dT- ( 1 + amoy)Qi = 0 Ddns id suite on néglige W et on conserve l’équation (11).

Table des matières

1 – INTRODUCTION
2 – EXIGENCES DE QUALITE DE L’AIR
2.1 – GENERALITES
2.2 – LES PRINCIPAUX POLLUANTS
2.21 – Tabagisme passif
2.22 – Radon
2.23 – Humidité de l’air
2.24 – Formaldehyde
2.25 – Produits de combustion
2.26 – Autres polluants
3 – LES MOTEURS DE LA VENTILATION
3.1 -LEVENT
3. – La nature du vent près du sol
3. – Variation de ia vitesse moyenne du vent avec la hauteur
3. – Champ de pression induit par le vent sur les constructions
3.2 – TIRAGE THERMIQUE
3.21 – Tirage thermique à travers une paroi verticale et notion äu plan neutre
3.22 – Tirage dans les conduits verticaux
3.3 – DISPOSITIFS MECANIQUES
4 – MODELISATION DES DIFFERENT CONSTITUANTS AERAULIQUES DU BATIMENT
4.1 – GENERALITES SUR LES ORIFICES
4.2 – BOUCHES D’ENTREES D’AIR ET D’EXTRACTION
4.21 – Bouche fixe
. 4.22 – Bouche autoréglable
4.23 – Bouche thermoréglable
4.24 – Bouche thermomodulante
4.25 – Bouche hygroréglable
4.3 – GRANDES OUVERTURE
4.31 – Schéma de principe
4.32 – Hypothèses et notations
4.33 – Calcul des débits échangés
4.34 – Modèle mathématique pour déterminer le coefficient
de décharge d’une grande ouverture
4.35 – Formules pratiques
4.4 – FEUILLURES DES OUVRANTS (portes et fenêtres)
4.5 • PAROIS OPAQUES – DEFAUTS D’ETANCHEITE.
4.51 -Perméabilité
4.52 – Perte de charge à travers un orifice percé dans
une paroi épaisse de surface infinie
4.53 – Modélisation de la perméabilité d’une paroi opaque
4.6 – CONDUITS DE VENTILATION
4.61 – Equation de Bemouilli généralisée
4.62 – Perte de pression totale dans un conduit cylindrique
long de section circuloire
4.63 – Pertes de chcrges singulières
4.7 – COURONNEMENTS DE CONDUITS VERTICAUX
4.71 – Equation odimensionnelle
4.72 – Relation entre les coefficients intervenant dans l’équation de GONZALEZ et ceux caractérisant actuellement les aspirateurs statiques en France
4.73 – Conclusion
4.8 – EXTRACTEURS MECANIQUES
5 – MODELISATION DES RESEAUX DE VENTILATION
5.1 – DEPERDITION THERMIQUE DES CONDUITS ET TIRAGE THERMIQUE
5. – Calcul des déperditions thermiques dans le conduit
5. – Expression du tirage thermique tenant compte des déperditions dans le conduit
5.2 – CAS DES APPAREILS A COMBUSTION RACCORDES
5.21 – Modélisation de la température du mélange d’air en aval d’une chaudière classique
6 – MOUVEMENTS D’AIR ENTRE ZONES
6.1 – MODELISATION
6. – Equation d’état
6. – Equation d’équilibre de l’air intérieur
6. – Champ de pression extérieur en présence du vent
6. – Lq mqsse de l’air à l’intérieur de chaque zone
6. – Equqtion de bilon de zones
6.16 – Equqtions d’écoulement
6.2 – CALCUL DES CONCENTRATIONS DE POLLUANTS
6.21 – Bilan masse de polluant
6.3 – MIGRATION D’HUMIDITE
6.31 – Migration de l’humidité dans les matériaux
6.4 – MISE EN FORME GLOBALE ET RESOLUTION NUMERIQUE
6.41 – Algorithmes de résolution
7 – DEVELOPPEMENT DE CODE DE CALCUL
7.1- NOTION DE MODELES FINALISES
7.2 – CODE DE CALCUL GAINE
7.21 – Objet
7.22 – Hypothèses spécifiques
7.23 – Données d’entrée du programme m
7.24 – Algorithme de résolution
7.25 – Fichier de sortie
7.3 – CODE DE CALCUL SIREN2
7.31 – Objet
7.32 – Hypothèses spécifiques
7.33 – Données d’entrée du programme
7.34 – Algorithme de résolution
7.35 – Fichier de sortie
8 – EXPLOITATION DES CODES DE CALCUL
6.1 – INTRODUCTION
8.2 • LOGEMENT HUIT ZONES : CALCUL EN REGIME PERMANENT (Conditions moyennes de températures et de pressions)
8.21 – Données d’entrée
8.22 – Résultats
8.23 – Conclusion
8.3 – INFLUENCE DE LA TURBULENCE DU VENT ET DE LA COMPRESSIBILITY DE L’AIR DES GRANDS VOLUMES SUR LA VENTILATION (maison individuelle)
8.31 – Introduction
8.32 – Champs de pression spatio-temporels
8.33 – Méthodologie
8.34 – Etude d’un logement comportant deux zones
8.35 – Etude d’un logement comportant une seule zone
(pièce à simple exposition)
8.36 – Conclusion
8.4 – INFLUENCE DES FLUCTUATIONS SPATIO-TEMPORELLES DU VENT SUR LE RESEAU DE VENTILATION
8.41 – Données d’entrée
8.42 – Résultats
8.43 – Conclusion
8.5 – ETUDE DES SYSTEMES DE VENTILATION
8.51 – Influence du diamètre du conduit d’extraction sur la
répartition des débits extraits (cas de VMC) 2
8.52 – Influence du coefficient de déperditions thermiques des conduits, des pertes de charge par confluence, de l’arrêt
de l’extracteur sur les débits d’extraction (cas de VMC Gaz)
8.53 – Influence des sections de grilles d’extraction sur la
répartition des débits extraits (conduits shunt)
8.54 – Recherche du dimensionnement adéquat du réseau de ventilation (maison individuelle)