Implémentation des modèles matériaux

Après l’adoption de deux approches pour la description du comportement des matériaux durant la mise en forme (cf. Chapitre2), des essais expérimentaux ont été réalisés pour l’identification des paramètres des différents modèles matériaux (cf. Chapitre3). Ce chapitre présente d’une part, l’implémentation de chaque modèle matériau dans ABAQUS afin de simuler la mise en forme des deux alliages avec les deux procédés détaillés précédemment (cf. Chapitre1) et d’autre part, la méthode d’identification des paramètres des modèles matériaux et leur validation par simulation numérique des essais constitutifs (traction, traction-compression, relaxation et fluage). Ce modèle matériau a été développé dans le cadre de la première approche détaillée précédemment (cf. Chapitre2). Il repose sur la description d’un comportement élasto-plastique, indépendant de la vitesse de déformation. Le critère de plasticité anisotrope de Hu2005 est adopté afin de prendre en compte le fait que les tôles sont laminées. La fonction de charge de ce critère est donnée par l’équation (IV.1). L’évolution mécanique du matériau durant l’écoulement plastique est décrite dans ce modèle par une loi polynomiale d’ordre 5 (équation (IV.2)) afin de représenter soit l’écrouissage isotrope soit l’adoucissement. La bibliothèque constitutive d’ABAQUS est vaste, mais, elle ne contient pas le critère de plasticité anisotrope de Hu2005. Pour cela, un programme (subroutine UMAT) a été développé afin d’implémenter ce modèle matériau élasto-plastique dans ABAQUS.

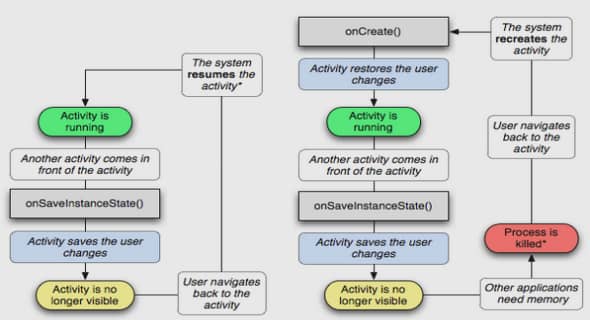
Implémentation du modèle dans ABAQUS

À chaque pas de temps ABAQUS fournit un incrément de déformation calculé à partir des états de contrainte et déformation obtenus au pas précédent. Après résolution du système d’équations Les figures ci-après représentent schématiquement l’algorithme contrôlant l’écoulement plastique. Celui-ci repose sur le principe du retour radial et a été implémenté, dans ABAQUS, via une subroutine UMAT 3D. Après une prédiction élastique basée sur l’incrément de déformation donné par ABAQUS, le retour sur la surface de charge s’effectue de manière itérative selon la normale à cette surface. L’algorithme utilise un formalisme implicite dont le critère de convergence est basé sur une valeur minimale d’un correcteur plastique. Le détail des équations et paramètres associés à la description du modèle élasto-plastique reposant sur le critère de Hu2005 est fourni en Annexe B, en particulier pour le calcul de la normale à la surface de charge et du correcteur plastique. Les sept paramètres du critère de plasticité anisotrope Hu2005 « Xi, i=1…7 » sont identifiés, pour chaque alliage, à partir des résultats des essais de traction suivant différentes directions de prélèvement (0°, 45° et 90°) et avec une vitesse de déformation de 10-2 s-1. Comme indiqué dans le Tableau IV-1, les paramètres du critère sont déterminés à partir d’équations faisant intervenir les coefficients d’anisotropie et les limites d’élasticité. Toutefois, pour deux paramètres (X3 et X6), une contrainte équibiaxiale est nécessaire. Elle est calculée à partir de l’équation (IV.3) donnée par Hu en 2005 (Hu, 2005).

Des éléments C3D8 avec une intégration totale ont été utilisés. La taille de chaque élément dans les éprouvettes plates, est de 3x3x1mm et 3x3x0.5 pour, respectivement, l’alliage 2050 et l’alliage AW551. Ces dimensions mènent à 4 éléments dans l’épaisseur, comme illustré en Figure IV-3. Pour les éprouvettes cylindriques (non montrées ici), la taille de chaque élément est de l’ordre de 2 mm3. La déformation de l’éprouvette est réalisée en imposant, sur un côté de l’éprouvette, un déplacement selon l’axe X tandis que l’autre côté demeure fixe. Le déplacement est réalisé de telle manière à assurer la bonne vitesse de déformation au sein du matériau. Afin de reproduire au mieux la configuration expérimentale, dans laquelle seule la partie centrale de l’éprouvette est chauffée, deux comportements différents ont été employés dans l’éprouvette : le modèle élasto-plastique dans la zone centrale (en orange sur la figure) et un comportement élastique pour le reste de l’éprouvette. La validation des paramètres identifiés s’effectue par comparaison des courbes expérimentales aux courbes issues de la simulation numérique. Se rajoute à cela une comparaison de ces résultats à ceux obtenus en utilisant un modèle standard d’ABAQUS, c.-à-d. un comportement élasto-plastique anisotrope décrit par une loi tabulée et le critère de Hill48. Pour ce dernier cas, deux jeux de paramètres ont été utilisés pour le critère de plasticité (Hill481 : paramètres identifiés avec la première méthode et Hill482 : paramètres identifiés avec la deuxième méthode (Tableau IV-2)).