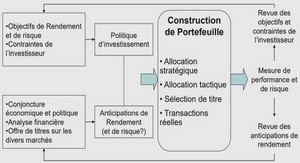
Théorie et Gestion de Portefeuille

Rentabilité d’un portefeuille
Exemple:
Vous constituez un portefeuille d’une valeur totale de 15000 € composé de 100 actions Michelin au prix unitaire de 60 €et 200 actions Carrefour au prix unitaire de 45 €. Un mois plus tard, le prix de l’action Michelin est de 66 €et celui de l’action Carrefour est de 42,75 €. est de 42,75 €. 1)Quelle est la valeur finale du portefeuille ? 2)Calculez la rentabilité du portefeuille de deux manières. 3)Quelles sont les nouvelles pondérations des titres si vous décidez de garder la même composition ?
1)Représenter l’ensemble des portefeuilles possibles pour des corrélations égales à 1 et -1. 2)Déterminer la rentabilité et la volatilité des portefeuilles composés respectivement de 100%; 80%; 60%; 40%; 20% et 0% du titre X (pour une corrélation nulle). 3)Représenter ces portefeuilles dans l’espace (espérance volatilité).

Nouvelle frontière efficiente
•Pour un niveau de risque donné, l’investisseur cherchant à obtenir la rentabilité espérée la plus élevée possible doit chercher la droite la plus pentue combinant l’actif sans risque et un PF appartenant à la frontière efficiente des actifs risqués. Cette pente pour un PF donné A correspond au ratio de Sharpe du PF.
Sharpe de Ratio
•Le ratio de Sharpe exprime la prime de risque offerte par le PF pour une unité de risque.
•La nouvelle frontière efficiente est la demi-droite passant par l’actif sans risque et tangente à la frontière efficiente des PF risqués.
•Le portefeuille tangent est le seul PF risqué efficient lorsqu’un actif sans risque existe.
•Théorème de séparation: Tous les investisseurs doivent détenir le même PF d’actifs risqués indépendamment de leur aversion pour le risque.
Nouvelle frontière efficiente
risqués indépendamment de leur aversion pour le risque.
•L’aversion pour le risque d’un investisseur détermine exclusivement la proportion de sa richesse investie dans le PF tangent.