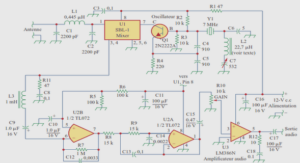
Faddeev and jackiw method for systems with constraint

Introduction In order to search for new much simpler methods to deal with constrainted systems, FaddeevJackiw proposed an alternative treatment seems technically di§erent and does not have the same Diracís conjecture, thus it has evoked much attention [3]. Noting that the original FaddeevJackiw method was addressed to unconstrained systems, while Barcelos-Neto and Wotzasek had been proposed an extension called symplectic algorithm to deal with constraints systems [9, 10], that we are dealing with it in this thesis. The Faddeev-Jackiw (F-J) formalism pursues a classical geometric treatment based on the sympletic structure of the phase space and it is only applied to Örst order Lagrangians, linear with respect to velocities [3]. This method is rised basically on Lagrangian formalism and the matrix form of Euler-Lagrange equations as a main source of studying, without missing an important passage in converting the Lagrangian to linear one with respect to velocities and conjugate momenta using the Legendre transformation. The matrix form of (E-L) equations lead us to introduce the (F-J) matrix that gives us two cases can be treated according to its determinant as we will see later. Thus, the objective of this chapter is to treat the (F-J) matrix cases with a symplectic algorithm step by step till we will end with an invertible matrix represent the basic geometric structure called generalized Poisson brackets and coincide with Diracís brackets, that will be the bridge to the commutators of the quantized theory, as we have already mentioned in the Faddeev and jackiw method for systems with constraints 4.2 Lagrangian linearization 23 previous chapter, while our real aim is to make a clear comparaison later between those methods in that crossing road.

Lagrangian linearization

As we have already evoked in the preceding chapter, we will not be able to express for a singular systems all velocities ( the q_i) according to the coordinates ( the qi), and the conjugate momenta (the pi) using the relations pi = @L=@q_i , i = 1; ::::; n. As we know in this case the Hessian matrix W is not invertible. Considering R = rank (W), this means that it is possible to reverse the equations pi = @L=@q_i only with respect to R generalized velocities q_a with a = 1; :::; R, writing them as functions of the other velocities, generalized coordinates and conjugate momenta as follows : q_a = fa (qi ; pb; q_s) , a; b = 1; :::; R , i = 1; ::; n , s = R + 1; :::; n 

Faddeev and Jackiw approach

Faddeev-Jackiw method is based on two main maneuvers i) The linearization of the Lagrangian with respect to the generalized velocities. ii) The inversion of the Faddeev-Jackiw matrix obtained using the (E-L) equations. This method allows to derive the set of Dirac brackets in one fell swoop without needing to calculate any Poisson brackets separately . The idea is to treat the independent variables ( the qi , i = 1; ::; n and the pa , a = 1; :::; R ), on an equal footing by introducing new variables i = qi , i = 1; ::; n and n+a = pa with a = 1; :::; R, in such a way that the Lagrangian (4.3) is writte