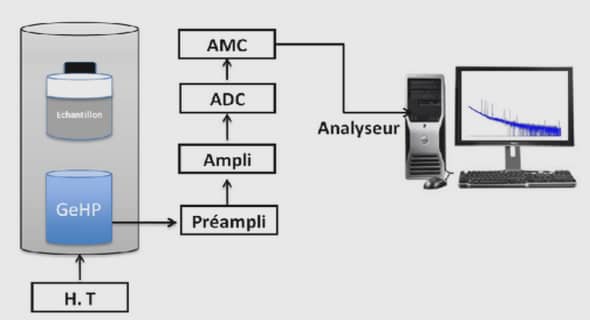
Extraction des capacités par méthodes intégrales

Dans ce deuxième chapitre, on présentera les formulations intégrales appliquées à notre problème d’électrostatique. Ces méthodes intégrales permettent de calculer des coeffi-cients d’interaction entre chaque élément de maillage des régions conductrices ou diélectriques (maillées en surface). Pour les calculs des coefficients d’interaction, différentes techniques de résolution de l’équation intégrale sont développées : une méthode de collocation ou une ap-en fonction des potentiels des conducteurs, la répartition des charges supposées être localisées au niveau des interfaces des conducteurs et des diélectriques. Enfin, une matrice de capacités peut être calculée à partir de ces charges présentes sur les conducteurs en tenant compte de la permittivité diélectrique du milieu environnant.Ce problème électrostatique peut être entièrement décrit par deux équations intégrales : celles du potentiel V et du champ électrique E dus aux charges présentes sur les conducteurs et les diélectriques. Le potentiel peut se calculer en tout point r de l’espace avec l’équation intégrale suivante :Maillage surfacique de deux conducteurs identiques de section rectangulaire, dont l’un entouré d’un matériau diélectrique, situés au-dessus d’un plan de masse – les nuances de couleurs sont dues à la valeur des charges surfaciques pour une répartition de potentiels donnée (conducteurs volumiques de gauche et droite fixés respectivement à 1 V et -1 V, et 0 V pour le plan de masse).

La méthode intégrale permet de projeter les équations du problème électrostatique sur le maillage des interfaces de tous les matériaux actifs. Cette mise en équations peut se mettre sous forme matricielle et conduit à la formation d’une matrice d’interaction pleine car un coefficient d’interaction non nul est calculé entre chaque élément de maillage.Dans notre problème électrostatique, ces interactions sont calculées entre chaque surface char-gée définissant l’interface d’un matériau conducteur ou d’un diélectrique. La figure II.1 montre,par exemple, le maillage en surface d’une géométrie composée de deux conducteurs identiques de section rectangulaire, dont l’un est entouré d’un matériau diélectrique, situés au-dessus d’un plan de masse.Pour garantir un potentiel uniforme à la surface des conducteurs les charges électriques se localisent dans les coins et sur les arrêtes et les bords des conducteurs. Par exemple, on peut observer ces effets de bords sur la figure II.1 ainsi que des effets d’ombrage sur le plan de masse.On parle d’interaction totale car chaque élément surfacique va interagir avec tous les autres comme le présente la figure II.2. Dans cette figure, les interactions représentées sont entre ba-rycentres mais pourraient être entre nœuds ou entre chaque surface des éléments, etc. Toutes ces variantes sont liées aux hypothèses de localisation des charges sur les éléments (illustrées à la figure II.3) et des techniques d’intégration comme les méthodes de collocation (ex : méthode des moments) ou de Galerkin. Par exemple, à l’ordre 0, les éléments sont supposés uniformément

Dans cette partie, on s’intéresse à une configuration de N conducteurs et diélectriques. Les matériaux sont supposés isotropes et parfaits. On suppose enfin que chacun des conducteurs est soumis à un potentiel V uniforme avec pour référence de potentiel un potentiel nul à l’infini.Dans ces conditions, on va s’intéresser aux équations écrites aux interfaces des conducteurs et des diélectriques.À l’interface conducteur-diélectrique, le potentiel est continu. Celui-ci peut se calculer en tout point r de l’interface (ou de l’espace) créé par les N conducteurs et diélectriques chargés de la façon suivante :Dans cette formule, ri représente le vecteur de coordonnées d’un point de la surface Si de charge surfacique σi ; ε0 est la permittivité du vide. Ainsi chaque matériau chargé surfaciquement contri- bue au calcul du potentiel de façon inversement proportionnelle à la distance qui la sépare du point de calcul.