Electricité générale
Exercice 5: BTS 2001 Etk Métro Amélioration du facteur de puissance avec un circuit LC (Solution 32:)
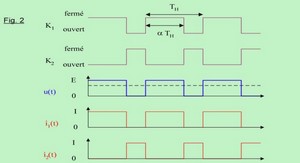
On s’intéresse à un fonctionnement de l’installation en pont tout thyristors. Sauf mention contraire (question 5.3), on admet que le courant i des figures 1 et 3 a l’allure représentée figure 7 sur le document réponse n°2.
La tension sinusoïdale du réseau a pour valeur efficace U = 400 V et pour fréquence f = 50 Hz.
1. Pour IC = 50 A, donner la valeur efficace I du courant i puis calculer la puissance apparente S de l’installation.
2. On rappelle que si la tension du réseau est sinusoïdale, la puissance active P et la puissance réactive Q qu’il fournit à l’installation se calculent en utilisant le fondamental (ou premier harmonique) du courant i.
2.1. Représenter sur le document réponse n°2, le fondamental iF du courant i sachant que son amplitude a pour valeur: IFMAX =
– Calculer la valeur efficace IF du fondamental pour Ic = 50 A.
– Indiquer la nature (avance ou retard) et la valeur du déphasage F du fondamental du courant par rapport à la tension du réseau.
2.2. Donner les expressions générales de la puissance active P et de la puissance réactive Q absorbées par l’installation.
Faire l’application numérique pour IC = 50 A et
En déduire la valeur numérique du facteur de puissance
3. D étant la « puissance déformante », on pose :
Calculer D avec les résultats des questions 1 et 2.2.
Comment faut-il agir sur les termes « Q » et « D » pour améliorer le facteur de puissance ?
On se propose maintenant de montrer qu’un circuit LC, branché aux bornes du réseau (fig. 1), agit à la fois sur la puissance réactive et la puissance déformante dans le but d’améliorer le facteur de puissance.
On donne : C = 200 F et L = 5,63 mH et on néglige la résistance de la bobine d’inductance L.
4. Action du circuit LC sur la puissance réactive
Cette action se manifeste sur le fondamental du courant i, c’est-à-dire pour la fréquence 50 Hz.
L’ensemble du montage est schématisé sur la figue 5. Le fondamental du courant consommé par l’installation est représenté par le générateur de courant iF.
4.1. Pour f = 50 Hz, calculer l’impédance complexe du circuit LC ; en déduire la valeur efficace du courant qui le traverse.
4.2. Calculer la puissance réactive QLC mise en jeu dans le circuit LC. On note sa valeur absolue. Préciser si est absorbée par le circuit LC ou fournie par lui au réseau.
4.3. Calculer la nouvelle puissance réactive Qt fournie par le réseau.
5. Action du circuit LC sur la puissance déformante
Cette action se manifeste sur le troisième harmonique du courant i, c’est à dire pour la fréquence 150 Hz. Pour expliquer le rôle du circuit LC on utilise le modèle représenté figure 6.
L’harmonique 3 du courant traversant l’installation est représenté par le générateur de courant iH3. On tient compte maintenant de l’impédance du réseau qui alimente l’installation et qui est équivalente à celle d’une inductance = 0,40 mH.
5.1. Pour f = 150 Hz, calculer l’impédance du circuit LC et la comparer à l’impédance présentée à cette même fréquence par l’inductance .
5.2. Montrer, sans calcul, que le réseau n’est pratiquement pas affecté par l’harmonique 3 de i. Quel est, dans l’expression de la puissance apparente S donnée à la question 4.3, le terme qui est modifié par cette action du circuit LC ?
5.3. Les figures 8 et 9 représentent les oscillogrammes des courants réellement mis en jeu dans l’installation lorsque le circuit LC est en place. Montrer en quelques lignes qu’ils confirment qualitativement l’analyse précédente.
5.4. Quels sont les appareils qui permettraient de compléter utilement l’usage de l’oscilloscope pour une confirmation quantitative ?