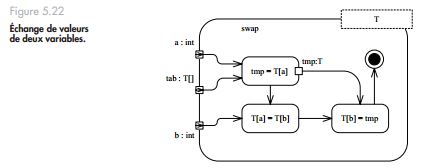
1. Utilisez une  variable temporaire  pour  stocker l’une des deux valeurs des variables à échanger avant de l’écraser en la remplaçant  par la valeur de l’autre variable. Ce dia- gramme met bien en avant le flot des valeurs. La variable temporaire  est représentée par un pin.

Comme vous n’avez pas plus de précisions sur le type des objets contenus dans le tableau, utilisez un template pour représenter ce type : l’opération est en effet générique et valable quel que soit le type T contenu dans le tableau.

2. Le diagramme de la figure 5.23 présente une structure intéressante pour la représentation de boucles, qui fait apparaître clairement les deux boucles imbriquées. Les cycles dans le graphe traduisent  le phénomène  de bouclage , et l’imbrication est visible grâce à la hiérarchie.

Le placement des objets constituant  les boucles (corps de boucle, condition  d’arrêt…) est reconnaissable visuellement ; il est réutilisé plusieurs fois dans les diagrammes qui suivent.

Deux points  de décision font apparaître  plus clairement  à la fois le début  et la fin de l’alternative dans la boucle interne.

Une nouvelle contrainte sur le type contenu dans le tableau impose que ce type soit muni d’une relation  d’ordre total pour  que puisse s’opérer la comparaison  de ses éléments. Indiquez-la en mentionnant que le type T doit réaliser l’interface Comparable. (Voir aussi la section 3.3 et l’exercice 4 du chapitre 3.)

3. Cette version du tri limite le nombre  de copies intermédiaires  de valeur. Elle réalise un  « roulement  » des variables (au lieu de les échanger deux à deux) qui déplace tout un bloc avant de recopier la variable temporaire.

La structure de l’algorithme reste assez proche du tri par bulles. De ce fait, il a la même complexité théorique en O(n2) en nombre d’opérations que le tri par bulles, mais réalise un  peu  moins  de copies que  lui. Vous vous en  apercevrez en  comparant  les deux schémas : l’imbrication des deux boucles apporte  le facteur n2 et les différences entre les actions dans chaque boucle n’apportent  qu’un facteur constant, donc théoriquement négligeable en complexité.

4. Le tri par fusion permet de montrer la modélisation de concepts algorithmiques avancés, en particulier la récursivité et le parallélisme. Ce type de tri est relativement puissant : il a une complexité comparable au quicksort, devenu standard,  et se prête également à une implémentation sur des listes chaînées. C’est récemment  devenu  l’algorithme de tri standard (au lieu de quicksort) du langage Perl par exemple.

Comme le montre le diagramme présenté à la figure 5.25, il est possible de l’implémenter avec des traitements en parallèle, ce qui se prête aux architectures parallèles. Pour autant, il n’est pas obligatoire de l’implémenter avec du parallélisme : toute exécution qui respecte l’enchaînement des actions et les barres de synchronisation est correcte.

Les numéros indiqués à côté des pins donnent  l’ordre des arguments. L’appel récursif est représenté comme un appel de fonction normal.

L’algorithme correspond à l’approche « diviser pour régner ». À chaque profondeur  dans l’appel récursif, vous triez un tableau deux fois plus petit : la moitié du tableau précédent. La complexité théorique totale des traitements  n’est qu’en O(n log n), au lieu de O(n2), comme les deux algorithmes précédents.