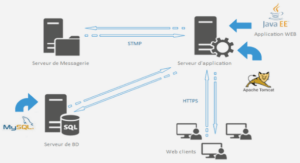
Etude et conception d’une application de chiffrement et de signature de documents

La structure multiplicative des entiers

Divisibilité

Définition 1.1 Soit a, b ∈ Z avec a 6=0. On dit que a divise b et on écrit a|b si b/a ∈ Z, c’est-à-dire si il existe k ∈ Z tel que b = ka. Dans ce cas, on dit aussi que b est divisible par a, ou que a est un diviseur de b ou que b est un multiple de a. Le lemme suivant établit quelques propriétés de base de la notion de la divisibilité : Lemme 1.2 Soit a, b ∈ Z avec a 6= 0. (a) Si a|b, alors soit b = 0 soit |b| a. (b) Si a|b et a|c, alors a|(bx + cy) pour tout x, y ∈ Z. (c) Si a|b et c|d, alors ac|bd. (d) Si a|b et b|c, alors a|c. (e) Si c 6= 0 et ac|bc, alors a|b. Un nombre ne divise pas toujours un autre. Par exemple, 3|6 mais 3 – 7. En général, on a le théorème suivant. Théorème 1.3 (Division euclidienne). Soit a, b ∈ Z avec a 6= 0. Il existe q, r ∈ Z uniques tels que b = qa + r et 0 ≤ r < |a|. Les nombres q et r sont appelés le quotient et le reste de la division de b par a, respectivement. Démonstration.Puisque qa =(-q)(-a) et| − a| = |a|, on peut supposer, sans perte de généralité, que a ≥ 1. On commence en prouvant l’existence de q et de r. On considère les nombres nj := b – ja, j ∈ Z. Observons que nj+1 – nj = -a, c’est-à-dire les nombres nj sont une progression arithmétique d’étape a.Donc il existe j0 ∈ Z tel que nj0 ∈ [0, a).(Sinon, on pourrait trouver j tel que nj+1 < 0 et nj ≥ a et, par la suite, nj – nj+1 > a, ce qui est impossible.) On pose r = nj0 ∈ [0, a) et on observe que b = j0a + nj0 . Donc l’existence de q et r découle en posant q = j0 et r = nj0. Finalement, on montre l’unicité de q et r. Supposons que b = qa + r = q0a + r0 avec 0 ≤ r, r0 < a. Donc (q – q0 )a = r0 – r, 4 ce qui implique que a|r0 – r . Cependant |r0 – r| < a par notre hypothèse que 0 ≤ r, r0 < a. Donc lemme (1.1.1.1) implique que r0 = r. Donc on trouve que (q – q0 )a = 0 et, puisque a ≥ 1, alors q0 = q aussi.

 Le plus grand commun diviseur

Définition 1.4 Soient a, b ∈ Z qui ne sont pas les deux égaux à 0. Le plus grand commun diviseur de a et b, dénoté par (a, b), est défini d’être le plus grand nombre naturel qui divise a et b. C’est-à-dire (a, b) = max {d ∈ N : d|a et d|b }. Remarque 1.5 Notre hypothèse que soit a 6= 0 soit b 6= 0 implique que l’ensemble { d ∈ N : d|a et d|b } est non-vide et fini. Donc (a, b) est bien défini. On peut utiliser un algorithme rapide pour calculer le plus grand commun diviseur de deux nombres qui se base sur la division euclidienne. L’observation-clé est donnée au lemme suivant : Lemme 1.6 Pour tout a, b, q ∈ Z avec a 6= 0, on a que (a, b) = (a, b – qa). En particulier, si r est le reste dans la division de b par a, on a que (a, b) = (a, r). Démonstration. Si d|a et d|b, alors d|b – qa aussi. Réciproquement, si d|a et d|b – qa, alors d|qa + (b – qa) = b. Donc on trouve que {d ∈ N : d|a et d|b } = { d ∈ N : d|a et d|b qa } ce qui termine la démonstration. Ce lemme nous amène à l’algorithme euclidien pour calculer le plus grand commun diviseur de deux nombres. Soient a, b ∈ N . Sans perde de généralité, on suppose que b ≥ a.On écrit b = qa + r avec 0 ≤ r < a pour que (a, b) = (a, r), ce qui nous permet de remplacer le pair (a, b) avec un nouveau par, (a, r), dont le plus petit élément est strictement plus petit qu’on avait avant. Bien sûr, on peut répéter cette procedure : on a que a = q0 r + r0 avec 0 ≤ r 0< r et que (a, r) = (r0 , r), ce qui nous permet de remplace le pair (a, r) avec le nouveau pair (r0 , r) pour que minr, r0 = r 0 < r = mina, r

Théorème 1.9

Soient a, b ∈ Z qui ne sont pas les deux égaux à zéro. Alors, le plus grand commun diviseur de a et b est une combinaison linéaire de a et b, c’est-à-dire il existe deux entiers x et y tels que (a, b) = ax + by. Démonstration. Le cas où a = 0 ou b = 0 est facile. Supposons maintenant que a et b ne sont pas zéro. Sans perde de généralité, on peut supposer que a, b ∈ N Donc, en utilisant la notation au-dessus, on a que (a, b) = bn, où b0 = q1b1 + b2, b1 = q2b2 + b3, b2 = q3b3 + b4,…, bn−2 = qn−1bn−1 + bn, Avec b0 = b et b1 = a. (a, b) = bn = bn−2 qn−1bn−1 est une combinaison linéaire de bn−1 et de bn−2. Puisque bn−1 = bn−3 qn−2bn−2 est une combinaison linéaire de bn−2 et de bn−3, on trouve que (a, b) a la même propriété. On continue en remplaçant bn−2 par bn4 qn−3bn−3 pour trouver que (a, b) est une combinaison linéaire de bn−3 et de bn−4. De façon inductive, on conclut que (a, b) est une combinaison linéaire de b0 et de b1, comme affirmé. 

Lemme 1.11

Soient d, a, b ∈ N Alors d|a et d|b si et seulement si d|(a, b). C’est-à-dire, chaque commun diviseur de a et b divise leur plus grand commun diviseur. Démonstration. Supposons que d|a et que d|b. On a que (a, b) = ax + by pour quelques x, y ∈ Z. Donc d|ax + by = (a, b), du lemme 1.2(b). Réciproquement, supposons que d|(a, b). Par définition, on a que (a, b)|a et que (a, b)|b. Donc lemme 1.2(d) implique que d|a et que d|b. Lemme 1.12 (ab, ac) = a · (b, c) Démonstration. Soit d = (ab, ac) et e = (b, c). On veut montrer que d = ae. Il suffit de montrer que d|ae et que ae|d. On a que e|b et que e|c. Donc ae|ab et ae|ac. Alors lemme 1.11 implique que ae|(ab, ac) = d. Réciproquement, on a que a|ab et que a|ac. Par la suite, a|(ab, ac) = d. On écrit d = ad0 et on observe que ad0 |ab et que ad0 |ac.Alors on trouve que d0 |b et que d0 |c, ce qui implique que d0 |(b, c) = e. Donc d = ad0 |ae, ce qui conclut la démonstration. Proposition 1.13 Soit a, b ∈ Z. Si d = (a, b), alors il existe k, l ∈ Ntels que a = dk, b = dl et (k, l) = 1. Démonstration. On sait que d|a et d|b, donc il existe k, l tels que a = dk et b = dl. De plus, on a que d = (a, b) = (dk, dl) = d · (k, l), d’après le lemme 1.12. Donc (k, l) = 1, comme affirmé, ce qui conclut la démonstration. 8 Proposition 1.14 (Lemme d’Euclid). Soient a, b, c ∈ N avec (a, b) = 1. Si a|bc, alors a|c. Démonstration. Puisque (a, b) = 1, alors il existe x, y ∈ Z tels que 1 = ax + by. Donc c = acx + bcy. On a que a|a et que a|bc. Par conséquent, on trouve que a divise leur combinaison linéaire acx + bcy = c. Ceci termine la démonstration. Lemme 1.15 Soient a, b, c ∈ N avec (a, b) = 1. Si a|c et b|c, alors ab|c. Démonstration. Soit c = ka. On a que b|c = ka et que (a, b) = 1. Donc le lemme d’Euclid nous donne que a|k. Alors, k = al pour un l ∈ N C’implique que c = lab, ce qui conclut la démonstration. Proposition 1.16 Soient a, b, c ∈ N avec (a, b) = 1. Si (a, c) = (b, c) = 1, alors (ab, c) = 1. Démonstration. Soit d = (ab, c). L’idée est que d ne peut pas avoir une partie commune ni avec a ni avec b car d|c. En effet, soit d1 = (d, a). On a que d1|d|c et donc d1|c. Alors d1|(a, c) = 1, ce qui implique que d1 = 1. Puisque (d, a) = 1 et d|ab, alors le lemme d’Euclid implique que d|b. Mais dans ce cas on a que d|(b, c) = 1, d’où on déduit que d = 1, comme affirmé.