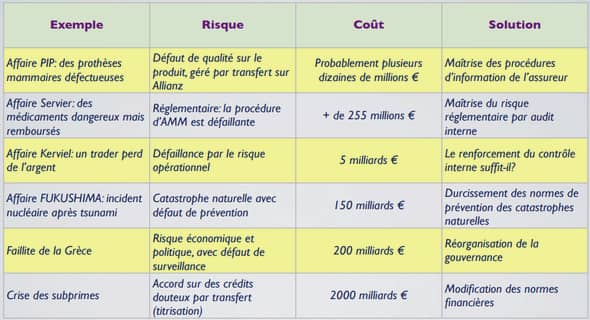
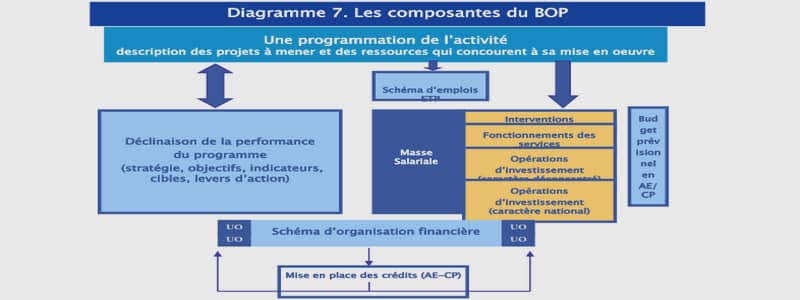
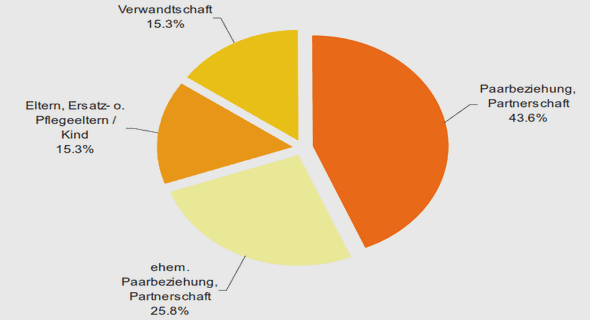
Ensembles minimaux pour le flot horocyclique sur une surface hyperbolique géométriquement infinie

Modèles du plan hyperbolique

De nombreux mathématiciens ont cherché à construire une géométrie qui contredit le cinquième postulat d’Euclide à savoir « par un point, on ne peut mener qu’une droite et une seule droite parallèle à une droite donnée ne contenant pas ce point ». C’est grâce aux travaux de Gauss, Lobatchevski, Bolyai, Riemann,… que les géométries non-euclidiennes firent leur apparition. D’abord considèrées comme des curiosités mathématiques, elles deviennent rapidement des outils fondamentaux de la physique théorique et plus tard des espaces propices d’étude en lien avec de nombreux domaines des mathématiques tels que les systèmes dynamiques auxquels nous nous intéressons. Cette thèse a pour cadre une de ces géométries non-euclidiennes : la géométrie hyperbolique en dimension deux. Elle admet plusieurs modèles parmi lesquels nous en retenons deux qui ont la particularité de conserver les angles euclidiens : le modèle du disque de Poincaré et celui du demi-plan de Poincaré. 

Modèles du plan hyperbolique 

 Le modèle du disque de Poincaré 

Présentation du modèle et de ses isométries 

La métrique : Le plus connu des modèles du plan hyperbolique est celui du disque de Poincaré, c’est le disque unité du plan complexe C ‘ R 2 D = {z = x + iy ∈ C : |z| < 1} muni de la métrique riemannienne dite hyperbolique, donnée par : ds2 = 4dzdz¯ (1 − zz¯) 2 = 4 dx2 + dy2 (1 − x 2 − y 2) 2 . (1.1) Cette métrique est déduite du produit scalaire sur l’espace tangent à D en tout point z, TzD : < u, v >z= 1 (1 − |z| 2) 2 < u, v > où u, v ∈ TzD et < u, v > est le produit scalaire usuel. Pour plus de simplicité nous écrirons dans la suite D au lieu de (D, ds). Notons qu’à l’aide de la métrique ds nous pouvons définir l’angle entre deux vecteurs tangents de D en un même point. Soit z ∈ D et soient u = (z, ~u), v = (z, ~v) ∈ TzD. Nous définissons l’angle entre ~u et ~v comme étant le réel θ ∈ [0, π[ vérifiant cos θ = < u, v >z k u kz . k v kz . De plus l’angle orienté entre ~u et ~v, noté ](~u, ~v) ou (~u, ~v) ∈] − π, π[ est défini en posant d’une part cos(~u, ~v) = < u, v >z k u kz . k v kz . et d’autre part en imposant la condition (~u, ~v) > 0 si et seulement si u1v2 − u2v1 > 0 où ~u = (u1, u2)z et ~v = (v1, v2)z. Soit ds2 0 = dzdz¯ = dx2 + dy2 la métrique euclidienne de C ‘ R 2 . Comme ds2 et ds2 0 sont proportionnels en tout point de D, alors la métrique ds est conforme puisque ds0 l’est. b) Les isométries de D : Parmi les transformations de D il y a une classe particulière à laquelle nous allons nous intéresser : les isométries de D. Définition 1.1. Une isométrie de D est une transformation de D qui laisse la métrique ds2 invariante. Une isométrie de D est dite isométrie positive si elle conserve les angles orientés. Dans le cas contraire nous dirons que l’isométrie est une isométrie négative. 

Proposition 

 Les isométries positives de D sont : 7 1. Modèles du plan hyperbolique – les rotations de centre 0 (z 7→ e iθz, θ ∈ R), – les restrictions à D des transformations de C du type : φ(z) = e i2α βz¯ + 1 z + β où α ∈ R et β ∈ C et | β |> 1. 2. Les isométries négatives de D sont : – les transformations z 7→ e iθz, θ ¯ ∈ R, – les restrictions à D des transformations de C du type : ψ(z) = e 2iα β¯z¯ + 1 z¯ + β où α ∈ R et β ∈ C et | β |> 1. Les isométries négatives de D sont les composés d’une isométrie positive de D par la conjugaison complexe z 7→ z. ¯ Démonstration : 1. – Une première classe de transformations de C conservant les angles orientés est celle des similitudes directes (z 7→ az + b). Pour qu’une telle similitude laisse D globalement invariant, il faut et il suffit que |a| = 1 et b = 0. Une telle similitude est donc une rotation de centre 0, z 7→ e iθz. Cette transformation laisse clairement ds2 invariant, et est donc une isométrie positive de D. – On sait que les transformations holomorphes (conservant donc les angles orientés) de D qui ne sont pas des similitudes directes sont des homographies z 7→ az+b cz+d où a, b, c, d sont des nombres complexe tels que ad − bc 6= 0, c 6= 0, voir [56]. Soit donc z 0 = az+b cz+d . On a dz0 = ad−bc c . dz (cz+d) 2 et : dz0dz¯ 0 (1 − |z 0 |) 2 = |ad − bc| 2 |c| 2 . dzdz¯ [(|c| 2 − |a| 2)zz¯ + (c ¯d − a¯b)z + (dc¯− ba¯)¯z − (|b| 2 − |d| 2)]2 . Pour que cette homographie soit une isométrie, il faut et il suffit que : c ¯d − a¯b = dc¯− ba¯ = 0, |c| 2 − |a| 2 = |b| 2 − |d| 2 , ad − bc| 2 |c| 2(|c| 2 − |a| 2) 2 = 1. La solution de ce système d’équations est a = ¯d, b = ¯c, |c| = 1. En posant c = e −iα et d = βc, on voit que de telles transformations du plan complexe laissant ds2 invariant sont du type : z 7→ φ(z) = e 2iα βz¯ + 1 z + β , α ∈ R, β ∈ C. 8 1. Modèles du plan hyperbolique Pour que l’application φ laisse D globalement invariant, il faut et il suffit que |z| < 1 implique que |φ(z)| < 1, soit |βz¯ + 1| 2 < |z + β| 2 . On a |βz¯ + 1| 2 = |β| 2 |z| 2 + 2Re(βz¯ ) + 1 et |z + β| 2 = |z| 2 + 2Re(βz¯ ) + |β| 2 . Les inégalités ci-dessus deviennent alors (|β| 2 − 1)(|z| 2 − 1) < 0. Elles sont satisfaites si et seulement si |β| > 1. 2. La même démarche ci-dessus appliquée aux similitudes indirectes (z 7→ az¯ + b) et aux anti-homographies z 7→ az¯+b cz¯+d où a, b, c, d sont des nombres complexe tels que ad − bc 6= 0, c 6= 0 montre que les isométries négatives de D sont : – la composée d’une rotation de centre 0 par une symétrie axiale d’axe passant par 0, z 7→ e iθz. ¯ , – la composée de φ par la conjugaison complexe z 7→ z¯ : z 7→ ψ(z) = e 2iα β¯z¯ + 1 z¯ + β α ∈ R, β ∈ C. ✷ La rotation de centre 0 et d’angle 2α s’écrit sous la forme z 7→ az+b ¯bz+¯a avec a = e iα, b = 0 et |a| 2 −|b| 2 = 1. De même l’isométrie positive z 7→ φ(z) = e 2iα βz¯ +1 z+β s’écrit également sous la forme φ(z) = az+b ¯bz+¯a , avec a = e iαβ¯ √ |β| 2−1 , b = e iα √ |β| 2−1 et |a| 2−|b| 2 = 1. Réciproquement, par un calcul, on montre que toute homographie de C du type z 7→ az+b ¯bz+¯a , avec |a| 2 − |b| 2 = 1, induit sur D une isométrie positive. On a donc la proposition suivante : 

Proposition 

 Les isométries positives de D sont les restrictions à D des homographies complexes de C du type z 7→ az+b ¯bz+¯a avec |a| 2 − |b| 2 = 1. Elles forment un groupe noté Isom+(D). b) Les isométries négatives de D sont les restrictions à D des anti-homographies complexes de C du type z 7→ az¯+b ¯bz¯+¯a avec |a| 2 − |b| 2 = 1. 1.1. 2 Distance et Géodésiques Définition 1.4. Soient I = [a; b] ⊂ R et c : I → D une courbe paramétrée, différentiable par morceaux : c(I) = {z(t) = x(t) + iy(t) ∈ D/t ∈ I}, La longueur hyperbolique de c notée l(c) est définie par : l(c) = Z c 2|dz| 1 − |z| 2 = Z b a 2 p (x 0(t))2 + (y 0(t))2 1 − (x(t))2 − (y(t))2 dt. (1.2) Définition 1.5. La distance hyperbolique, notée ρ, induite par la métrique hyperbolique 9 1. Modèles du plan hyperbolique entre deux points z et z 0 de D est définie par : ρ(z, z0 ) := inf c l(c), (1.3) où la borne inférieure est prise sur l’ensemble des courbes c différentiables par morceaux incluses dans D reliant z et z 0 . On remarquera que pour tout g ∈ Isom+(D), l(g(c)) = l(c) et ρ(g(z), g(z 0 )) = ρ(z, z0 ). Définition 1.6. Une géodésique de D est une courbe différentiable par morceaux c : I =]a, b[→ D telle que pour tout couple de points distincts sur c(I), la courbe c réalise la borne inférieure des longueurs des courbes passant par ces deux points. C’est-à-dire, ∀ t1, t2 ∈]a, b[, ρ(c(t1), c(t2)) = l[c(t1), c(t2)] où l[c(t1), c(t2)] désigne la longueur hyperbolique entre les points c(t1) et c(t2). Le théorème suivant nous donne la description géométrique des géodésiques de D. Théorème 1.7. Les géodésiques de D sont les demi-cercles euclidiens de D orthogonaux à S 1 = {z ∈ D : |z| = 1} et les diamètres euclidiens de D. Démonstration : Tout d’abord, montrons que le diamètre euclidien ]−1, 1[= R∩D est une géodésique de D. Soient a et b deux nombres réels tels que −1 < a < b < 1. Considérons un arc de courbe c d’équation z(x) = x + iy(x) joignant a à b, donc tel que y(a) = y(b) = 0. Nous avons l(c) = Z b a 2 p 1 + (y 0(x))2 1 − x 2 − y 2 dx ≥ Z b a 2 1 − x 2 − y 2 dx ≥ Z b a 2 1 − x 2 dx =  » ln 1 + x 1 − x #b a . puisque  » ln 1+x 1−x #b a est la longueur du segment [a, b] ce segment [a, b] minimise la distance entre a et b. Soit maintenant c une géodésique reliant a et b. La première inégalité ci-dessus est donc une égalité et nous en déduisons que la coordonnée y(x) de c est constante et est égale à 0. D’où l’unique géodésique reliant a et b est le diamètre ] − 1, 1[ de D. Les rotations de centre O étant des isométries, elles transforment toute géodésique en une géodésique, donc tous les diamètres de D sont des géodésiques. Considérons un arc de cercle α orthogonal à S 1 en ses extremités. Quitte à effectuer une rotation de centre O, on peut supposer que son centre est sur l’axe réel négatif. Soient I et I’ les points d’affixes i et −i, A et A’ les extremités de α, voir 1.1. Soit Ω le point 10 1. Modèles du plan hyperbolique d’intersection des droites (IA) et (I’A’) avec l’axe réel. Notons a l’affixe de Ω, a ∈ [−∞, −1[. En utilisant les rapports de Thalès dans un triangle euclidien nous avons A( 2a 1+a 2 + i a 2−1 a 2+1 ) et A0 ( 2a 1+a 2 − i a 2−1 a 2+1 ). Posons ψ(z) = a + a 2 − 1 z¯ − a . Cette inversion ψ de pôle Ω et de puissance a 2 − 1 est telle que ψ(I) = A et ψ(I 0 ) = A0 donc elle transforme le segment [II’] en l’arc α. Nous avons pour tout z ∈ D ψ(z) = a + a 2 − 1 z¯ − a = az¯ − 1 z¯ − a Comme | a |> 1, ψ est de la forme donnée par la proposition 1.2 pour les isométries négatives de D. L’image α de la géodésique [II’] par l’isométrie ψ est donc également une géodésique. ✷ Figure 1.1 – Géodésiques de D On déduit du théorème ci-dessus les faits suivants, voir [14]. 1. Par deux points distincts ξ et η de S 1 il passe une unique géodésique notée (ξ, η) ou (η, ξ) et appelée souvent géodésique complète. 2. Par un point z de D et un point ξ ∈ S 1 il passe une unique géodésique. La partie de cette géodésique comprise entre z et ξ est appelée rayon géodésique et est notée [z, ξ). 3. Par deux points distincts z et z 0 il existe une unique géodésique qui les relie. La partie de cette géodésique comprise entre les points z et z 0 est appelé segment géodésique et est notée [z, z0 ] ou [z 0 , z]. Une géodésique complète sépare D en deux composantes connexes. Chacune de ces composantes est appelée demi-plan. Dans la suite lorsque nous dirons arc géodésique celà peut être une géodésique complète ou un rayon ou un segment géodésique. Pour finir cette sous-section précisons la notion l’angle formé par deux arcs géodésiques du plan hyperbo11 1. Modèles du plan hyperbolique lique. Soient deux courbes différentiables α1 et α2 qui se coupent en un point z de D. En choisissant des paramétrisations appropriées des courbes α1 et α2, on peut supposer que α1(0) = α2(0) = z. Définition 1.8. L’angle orienté entre les courbes α1 et α2 qui se coupent au point z est défini comme étant l’angle formé par les vecteurs ~v1 = α 0 1 (0) et ~v2 = α 0 2 (0) modulo π. 1.1. 3 Actions du groupe Isom+(D) sur D et T 1D Dans cette sous-section nous décrivons l’action de Isom+(D) sur D et sur le fibré unitaire tangent T 1D de D puis nous définirons une distance sur T 1D avant de donner des formules explicites de la distance ρ sur D. Proposition 1.9. L’action de Isom+(D) sur D est transitive. Démonstration : Il suffira de montrer que pour tout z ∈ D, il existe g ∈ Isom+(D), avec g(w) = aw+b ¯bw+¯a , tel que g(0) = z. On vérifie que l’élément g tel que a = √ 1 1−|z| 2 et b = √ z 1−|z| 2 convient. ✷ Le fibré tangent à D, TD = ∪z∈DTzD est la réunion des espaces tangents à D, TzD. Le fibré unitaire tangent est défini par T 1D = {u = (z, ~u) ∈ TD / k ~u k= 1}. L’action de Isom+(D) se prolonge sur T 1D de la façon suivante. Définition 1.10. L’action de Isom+(D) sur T 1D est définie par : g.u = g.(z, ~u) = (g(z), Tzg(~u)) = (g(z), g0 (z)~u) où g ∈ Isom+(D), (z, ~u) ∈ T 1D et Tzg est la différentielle de g au point z. Si ~u ∈ TzD est un vecteur tangent au point z son image par Tzg est g 0 (z)~u, c’est-à-dire le vecteur tangent à g(z) obtenu en tournant ~u d’un angle égal à arg(g 0 (z)) puis en le multipliant par le réel |g 0 (z)|. Proposition 1.11. Le groupe Isom+(D) agit simplement transitivement sur T 1D. Démonstration : Soient u, v ∈ T 1D. Supposons u = (0, ~u) et v = (z, ~v). D’aprés la proposition 1.9 il existe un élément γ de Isom+(D) tel que γ(0) = z. Notons 2θ la mesure de l’angle (T0γ(u), v). Soit r la rotation de centre 0 et d’angle θ. Nous avons : γ ◦ r(u) = v, donc Isom+(D) agit transitivement sur TD. Par ailleurs si g(u) = u alors g(z) = e iαz. La différentielle de g 12 1. Modèles du plan hyperbolique en 0 est la rotation vectorielle d’angle −2α et T0g(u) = u donc g = Id. Ceci montre que Isom+(D) agit simplement transitivement sur T 1D. ✷ Lemme 1.12. Soient α et β deux géodésiques de D. Il existe une isométrie positive g de D envoyant α sur β. Démonstration : Soit L =] − i, i[ le diamètre des imaginaires de D. Il suffit de montrer qu’il existe une isométrie positive de D envoyant L sur β. Si β est un diamètre alors la rotation de centre O et d’angle l’angle orienté (L, β) formé par les diamètres L et β est une isométrie positive g de D qui envoie L sur β. Supposons maintenant que β est un demi-cercle orthogonal à S 1 . Nous avons vu au cours de la démonstration du théorème 1.7 qu’il existe une inversion ψ envoyant L sur β, ce qui termine la preuve. ✷ Proposition 1.13. Soit un élément u = (z, ~u) de T 1D. Il existe une et une seule géodésique de D passant par z et tangent au vecteur ~u. Démonstration : Si le vecteur ~u est porté par un diamètre de D alors le diamètre passant par z est une géodésique tangente à ~u et il n’y a pas d’autre tel diamètre ni de demi-cercle orthogonal à S 1 et tangent à ~u. Si ~u n’est pas porté par un diamètre de D, puisque l’action de Isom+(D) sur D est transitive il existe une isométrie positive h telle que h(z) = 0. Soit r la rotation de centre 0 qui amène le vecteur ~u sur un vecteur ~v d’un diamètre α de D. Nous avons r ◦ h(z, ~u) = (0, ~v). D’aprés la première partie de cette démonstration le diamètre α est l’unique géodésique de D passant par 0 et tangent au vecteur ~v. L’isométrie positive h −1 ◦ r −1 envoie le diamètre α sur un unique demi-cercle de D perpendiculaire à S 1 . Cette géodésique passe par z et est tangent au vecteur ~u. D’où le résultat. ✷ Remarque 1.14. Puisqu’un élément de T 1D définit une unique géodésique alors d’aprés la proposition 1.11 l’action de Isom+(D) sur l’ensemble des géodésiques de D est transitive. On déduit de l’action transitive de Isom+(D) sur l’ensemble des géodésiques de D la proposition suivante, capitale entre autre dans la sous-section 4.2 du chapitre 2. 13 1. Modèles du plan hyperbolique Proposition 1.15. (voir [14] th.1.1.5 et th.1.1.6) 1. Si α˜ est une géodésique et z est un point de D n’appartenant pas à α˜ alors il existe une unique géodésique passant par z et perpendiculaire à α˜. 2. Si α˜ et β˜ sont deux géodésiques disjointes, alors il existe une unique géodésique perpendiculaire à α˜ et à β˜. Définissons maintenant une distance sur T 1D. Pour tout u ∈ T 1D on note (u(t))t∈R le paramétrage par longueur d’arc de la géodésique définie par u. Proposition 1.16. L’application D : T 1D × T 1D −→ R + définie par D(u, v) = Z +∞ −∞ e −|t| ρ(u(t), v(t))dt (1.4) où ρ est la distance hyperbolique sur D, est une distance sur T 1D invariante par Isom+(D). Démonstration : En posant f(t) = e −|t|ρ(u(t), v(t)) nous avons d’un côté 0 ≤ f(t) ≤ (2|t|+ρ(u(0), v(0))e −|t| . Donc la fonction f est intégrable sur R. Et de l’autre côté en utilisant le fait que ρ est une distance invariante par Isom+(D) nous avons pour tous u, v et w appartenant à T 1D et g ∈ Isom+(D) : – D(u, v) = 0 ⇔ u = v, – D(u, v) ≤ D(u, w) + D(w, v), – D(u, v) = D(v, u) et – D(gu, gv) = D(u, v). D’où l’application D est une distance sur T 1D, invariante par Isom+(D).