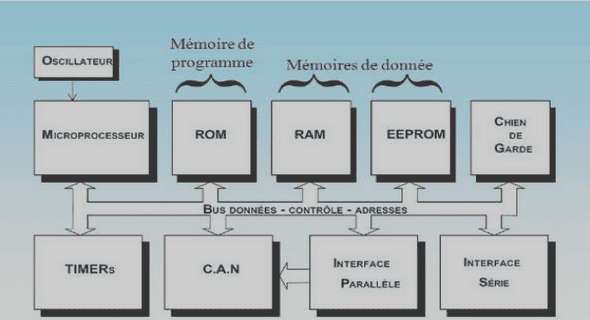
Diagramme du modèle de l’hélicoptère

L’hélicoptère est défini comme étant constitué de plusieurs sous-systèmes dont le fuselage, le rotor principal, le rotor de queue, l’empennage, le moteur,… La Figure ci-dessous illustre le diagramme du modèle de simulation d’un hélicoptère et ces différents sous-systèmes. Diagramme du modèle d’un hélicoptère et ces sous-systèmes .

Equation d’état de l’hélicoptère

Les équations globales de l’hélicoptère en mouvement sont des dérivées. Les forces et les moments des différents éléments d’un hélicoptère, comme le rotor principal, le rotor de queue, le fuselage et l’empennage, sont discutés dans cette section. L’hélicoptère a six degrés de liberté dans son mouvement et il a neuf variables générales, qui sont 𝑢, 𝑣, 𝑤 les composantes de la vitesse des aéronefs dans le centre de gravité, 𝑝, 𝑞, 𝑟 taux de roulis, de tangage et de lacet de l’aéronef sur les axes du corps de référence, et 𝜑, 𝜃, 𝜓 les angles d’Euler. Pour dériver les équations des mouvements de translation et de rotation d’un hélicoptère, l’hélicoptère est considéré comme un corps rigide autour d’un système d’axe fixé au centre de masse de l’aéronef, de sorte que, les axes se déplacent avec le temps de variation de la vitesse des composants sous l’action des forces appliquées. Les angles d’Euler définissent l’orientation du fuselage par rapport à la masse du système d’axes. Il y a quatre entrées de commande, qui sont : le bâton cyclique longitudinal (𝜂1𝑠), le manche cyclique latérale (𝜂1𝑐), le levier de pas collectif (𝜂𝑐), et la pédale d’entrée (𝜂𝑝), qui contrôle le mouvement de l’hélicoptère par rapport à 𝑋, 𝑌, 𝑍, 𝐿, 𝑀 et 𝑁. Ainsi, les équations du système sont les suivantes : ♣ Les dérivés des six premières variables d’état sont reliés aux six variables d’état. En effet, on a : 𝑥̇ = 𝑢 𝑦̇ = 𝑣 ∅̇ = 𝑝 𝜃̇ = 𝑞 𝑧̇ = 𝑤 𝜓̇ = 𝑟 . Les six autres équations sont obtenues en appliquant la relation fondamentale de la dynamique.