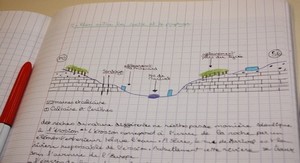
Description de la géométrie 

 Dans notre travail, on va simuler l’effet d’irradions d’une solution aqueuse d’ADN par les photons, la géométrie simulée se présente par un ADN plasmidique contenu dans une solution aqueuse, cette dernière est entourée par l’air puis un blindage fermé en polymère PMMA (polymethylmetacrylate) qui a pour objectif de réduire la pénétration des rayonnements en dehors du dispositif. Les rayonnements sont générés à partir d’une source de photons situés en dehors du dispositif, les photons primaires coupent quelques centimètres selon un trajet dirigé par un collimateur en cuivre avant d’interagir avec le filtre d’aluminium. Les rayonnements transmissent à partir de filtre rencontre un milieu aéré avant d’accès au milieu aqueux (cible) défini précédemment.  Description de la source Une source de photons caractérisée par une énergie variable, E= 0.04, 0.05, 0.1, 0.5, 0.1 MeV. Elle prend la forme d’un disque de r=0.8 mm de diamètre.  Description de collimateur Un collimateur de cuivre 63Cu (ρ= 8.94 g /cm3 ) avec une forme rectangulaire et une épaisseur d=2cm.  Description de filtre d’aluminium Ce filtre d’aluminium caractérisé par une densité massique ρ= 2.7 g /cm3 est situé à une distance de 1cm de la source. Il prend une forme conique avec un grand diamètre r1= 1.5 cm et un petit diamètre r2= 0.8 cm.  Description de blindage PMMA C’est une matière polymère de densité massique ρ=1.19 g/cm3 utilisée comme blindage pour objectif de réduire la pénétration des rayonnements ionisants en dehors du dispositif au but de protéger l’utilisateur. 

Description de la cible

 La cible est définie comme une solution aqueuse de volume total V=1cm3 qui contient un mélange de 10% d’ADN plasmidique (ρ=1,407 g/cm3 ) et 90 % d’eau (ρ=1g/cm3 ). L’ADN plasmidique PUC19 se caractérise par 2686 Pb et une masse atomique de 6 1,77 10  Da .

Simulation et résultats 

À l’aide du code PHITS de simulation Monte Carlo, plusieurs paramètres physiques peuvent être déduits. Dans la présente expérience, on a limité le choix pour calculer la Chapitre 4 Simulation et résultats 44 variation de la dose déposée par les électrons secondaires générés à la suite de l’interaction des photons X avec la matière pour des énergies différentes (0.04, 0.05, 0.1, 0.5, 0.1 MeV) dans un intervalle allant de la source jusqu’à la cible, afin de trouver une énergie capable à atteindre la cible d’ADN dans les limites de notre géométrie. Nous rappelons que les électrons secondaires traversent les molécules d’air en premier temps puis un filtre d’aluminium, jusqu’à il arrive à rencontrer un milieu aqueux contient de l’ADN. Pour cela, on a utilisé les tallies [t-gshow], [t-track], [t-deposit] pour obtenir les résultats ci-dessous. A l’aide de [t-gshow], on obtient la figure ci-dessous qui représente la géométrie étudiée en forme bidimensionnelle : Figure 15: Géométrie en deux dimensions Par la suite, On montre la variation de l’énergie déposée des électrons secondaires en fonction de Z (cm) pour différentes énergies de photons X incidents (0.04, 0.05, 0.1, 0.5, 0.1 MeV). 

Interprétation des résultats

 Les figures ci-dessus représentent la distribution de dose le long de la direction Z de faisceau. L’évolution de ces courbes peut être décomposée en trois régions principales : 

La région avant le filtre 

une incidence des électrons secondaires générés par les interactions des photons avec les composantes de l’air, apparaît à l’entrée du milieu absorbant. Ensuite, à cause de l’accumulation de la dose absorbée, une croissance de dose apparaît parallèlement avec l’augmentation de la profondeur jusqu’à atteindre une valeur maximale dans le filtre d’aluminium. D’autre part, la valeur initiale de la dose absorbée augmente proportionnellement avec l’énergie du faisceau incident ; aussi, plus l’énergie de photon incident est grande plus le parcours des électrons secondaires est important. Dans les littératures, cette région est appelée « Build-up region ». 

L’équilibre électronique 

un équilibre électronique est atteint dans un épaisseur donné, où le nombre d’électrons arrachés est équivalent au nombre d’électrons arrêtés. En Chapitre 4 Simulation et résultats 51 revanche, la distance de l’entrée de milieu jusqu’au point d’équilibre électronique Zmax (la région de filtre dans notre cas) est égale au parcours des électrons crées par les photons dans le milieu (à travers la région Build up).

La décroissance

Après l’équilibre électronique, la dose absorbée diminue lorsqu’il y a plus d’électrons arrêtés que d’électrons créés