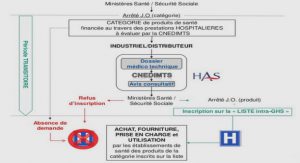
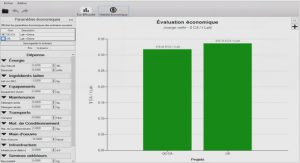
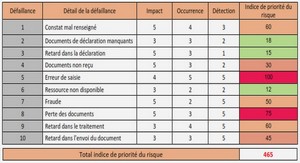
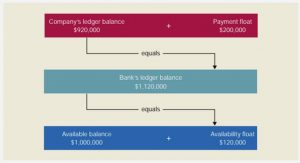
L’introduction au cours de probabilité vise à familiariser les étudiants avec les concepts de base et les méthodes de calcul des probabilités.
On appelle processus poissonnien (ou processus de Poisson), le modèle probabiliste des situations qui voient un flux d’évènements se produire les uns à la suite des autres de façon aléatoire (dans le temps et dans l’espace), obéissant aux conditions suivantes :
– la probabilité de réalisation de l’évènement au cours d’une petite période ou sur une petite portion d’espace Dt est proportionnelle à Dt soit pDt.
– elle est indépendante de ce qui s’est produit antérieurement ou à côté,
– la probabilité de deux apparitions sur le même Dt est négligeable.
Ainsi, des évènements qui se réalisent de façon aléatoire comme des pannes de machines, des accidents d’avions, des fautes dans un texte, …peuvent être considérés comme relevant d’un processus poissonnien.
Lois discrètes :
Par définition, les variables aléatoires discrètes prennent des valeurs entières discontinues sur un intervalle donné. Ce sont généralement le résultat de dénombrement.
Une distribution de probabilité suit une loi uniforme lorsque toutes les valeurs prises par la variable aléatoire sont équiprobables. Si n est le nombre de valeurs différentes prises par la variable aléatoire,
Découvrir une liste des cours probabilité et statistique, vous pouvez télécharger des cours statistiques pdf sur les propriétés générales de probabilités et statistiques, vous allez aussi pouvoir améliorer vos connaissances en probabilités et statistiques terminale sans difficultés. Aussi une sélection des meilleurs formations et cours avec exercices corrigés pour apprendre Probabilités & Statistiques.
Population et échantillons :
Considérons une ville d’un million d’habitants. Pour sonder la population nous pouvons interroger un échantillon de seulement mille personnes tirées au hasard.
A partir de cet échantillon de n=1000 individus, nous pouvons, grâce à la statistique, avoir des informations sur la population toute entière. Plus la taille de l’échantillon
est grand, plus les résultats seront précis. Nous appelons x la moyenne de l’échantillon et s son écart-type. Pour la population nous notons μ (lettre grec mu) la moyenne et σ (sigma) l’écart-type. Plus l’échantillon est grand, plus les valeurs de x et de s de cet échantillon sont amenées à se rapprocher de celles μ et σ de la population.
THÉORÈME CENTRAL LIMITE :
Nous prélevons au sein d’une population des échantillons aléatoires de taille n, la moyenne de l’échantillon x varie autour de la moyenne de la population μ avec un écart type égal à σ/√n, où σ est l’écart-type de la population.
Quand n croît la distribution d’échantillonnage de x est de plus en plus concentrée autour de μ et devient de plus en plus proche d’une distribution de Gauss.
Définition d’une distribution continue :
Il existe des grandeurs fondamentalement continues. Le temps en est une. Le temps s’écoule continument tel un fluide, il ne saute pas d’une valeur à l’autre. S’il
semble parfois égrainer les secondes, comme les perles d’un chapelet, cela n’est dû qu’à l’appareil de mesure insuffisamment précis. Par contre quand nous lançons un dé six faces, impossible de dire « j’ai fait 2,35 ! », c’est une valeur interdite, seules les valeurs entières de un à six sont permises.
Loi de Bernoulli :
• Soit une expérience aléatoire ayant deux résultats possibles :
le succès (probabilité p) ou l’échec (q=1-p)
• Famille de 4 enfants dont les deux parents sont porteurs d’un gène d’une maladie héréditaire (récessive).
• La v.a. « avoir la maladie m » suit une loi de Bernoulli de paramètre p égal à 0.25
• E(X) = p V(X)= p(1-p)
Loi binomiale :
• On répète n fois dans des conditions identiques une expérience aléatoire dont l’issue se traduit par l’apparition ou la non apparition d’un événement A de probabilité p, le résultat de chaque expérience étant indépendant des résultats précédents.
• Soit X le nombre d’apparitions de l’événement A parmi ces n expériences ( 0 ≤ X ≤ n).
• X suit une loi binomiale de paramètres n et p. B (n; p)