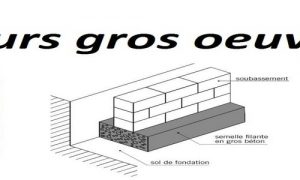
Cours gros oeuvre notions de résistance des matériaux

Poutre continue en BETON ARME
Généralité
On a remarqué qu’en utilisant les méthodes de R.D.M (Méthodes des forces ; Théorème des trois moments) pour les poutres continues en B.A, les résultats obtenus ne coïncidaient pas avec la réalité.
En particulier les moments sur appuis sont surestimés. Cela vient du fait que les méthodes de R.D.M
Ne tiennent pas compte de la variation d’inertie de la poutre en béton ( inertie différente en travée et sur appui )
Ne tient pas compte du caractère fluant du béton.
Est trop parfaite puisqu’elle tient compte des charges situées sur des travées éloignées de la travée considérée, alors que le béton amorti rapidement les effets.
Par conséquent pour les poutres en B.A il existe 2 méthodes
Méthode forfaitaire Méthode Caquot
Remarques
Calculs envisagés à l’ELU ou à l’ELS.
Ne concerne que les poutres associées à un plancher ou dalles calculées en flexion dans un seul sens.
Méthode forfaitaire. Art b.6.2,21 page 149
Domaine d’utilisation. artB.6.2,210

1. a) Applicable aux planchers à charges d’exploitation modérée: QB soit G : charges permanentes

Il faut  QB £ 2G
Ou
QB £ 5 kN/m2

1. b) Travées ayant même inertie.
2. c) Les portées successives sont dans un rapport compris entre 0,8 et 1,25.
3. d) Fissuration peu nuisible.

Ces quatre conditions sont impératives  pour utiliser cette méthode forfaitaire définie ci- après.
Principe de la méthode. artB.6.2,211
Principe de la méthode basé sur le phénomène d’adaptation des poutres en B.A
On évalue les moments maxi sur appuis et en travées en fonction du moment de flexion maxi Mo de la travée iso associée (avec le même chargement). Les moments correspondent à une fraction de Mo
Mt = kt x Mo              Mt moment en travée
Ma = ka x Mo             Ma moment sur appui
Les coefficients kt et ka sont choisis forfaitairement dans les plages définies au 2.3
Démonstration
Soit la poutre sur appuis simples
………

Si le lien ne fonctionne pas correctement, veuillez nous contacter (mentionner le lien dans votre message)
Cours gros oeuvre notions de résistance des matériaux (2,00 MO) (Cours DOC)