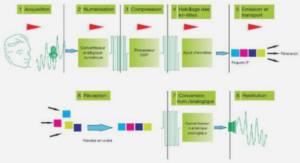
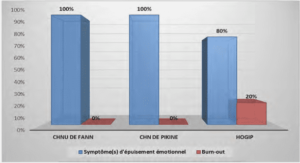
Changement de modèle, hétéroscédasticité, erreurs corrélées et estimation par moindres carrés généralisés

Changement de structure

Ici on considère que le choix du modèle linéaire inialement posé n’est pas convenable, à savoir que IEb Y 6= Xθ,donc que le modèle n’est pas Y = Xθ+ε. Nous allons voir tout d’abord comment détecter un tel diagnostic, puis comment le résoudre. Diagnostic d’une nécessité de changement de structure Essentiellement le graphe (b Yi,b εi). Changement continu de modèle En régression linéaire simple, la confrontation graphique entre le nuage de points (zi,yi) et la droite de régression de Y par Z par moindres carrés ordinaires donne une information quasi exhaustive.

Sur ce graphique, on voit une courbure de la “vraie” courbe de régression de Y et on peut penser que le modèle est inadéquat et que le premier postulat P1 n’est pas vérifié. •Dans le cas de la régression multiple, ce type de graphique n’est pas utilisable car il ya plusieurs régresseurs. Les différents postulats sont à vérifier sur les termes d’erreur εi qui sont malheureusement inobservables. On utilise leurs prédicteurs naturels, les résidus : b εi = Yi −b Yi. Par exemple, pour le modèle général de régression, Yi = µ + β1Z(1) i +···+ βpZ(p) i + εi, pour i = 1,··· ,n, =⇒ b εi = Yi −b µ−b β1Z(1) i −b β2Z(2) i −···−b βpZ(p) i pour i = 1,··· ,n. Le graphique le plus classique consiste à représenter les résidus (b εi)i en fonction des valeurs prédites (b Yi)i. Ce graphique doit être fait pratiquement systématiquement. Cela revient encore à tracer les coordonnées du vecteur P[X]⊥.Y en fonction de celles de P[X].Y. L’intérêt d’un tel graphe réside dans le fait que si les quatre postulats P1-4 sont bien respectés, il y a indépendance entre ces deux vecteurs qui sont centrés et gaussiens (d’après le Théorème de Cochran). Cependant, à partir de ce graphe, on ne pourra s’apercevoir que de la possible déficience des postulats P1 et P2, les deux autres postulats pouvant être « contrôlés » par d’autres représentations graphiques (voir plus loin). Concrètement, si on ne voit rien de notable sur le graphique (c’est-à-dire que l’on observe un nuage de points centré et aligné quelconque), c’est très bon signe : les résidus ne semblent alors n’avoir aucune propriété intéressante et c’est bien ce que l’on demande à l’erreur. Dans ce cas on peut penser que le modèle n’est pas adapté aux données.

En effet, il ne semble pas y avoir indépendance entre lesb εi et les b Yi (puisque, par exemple, lesb εi ont tendance à croître lorsque les b Yi sont dans un certain intervalle et croissent). Il faut donc améliorer l’analyse du problème pour proposer d’autres régresseurs pertinents, ou transformer les régresseurs Z(i) par une fonction de type (log,sin), ce que l’on peut faire sans précautions particulières. • On peut librement transformer les régresseurs Z(1),··· ,Z(p) par toutes les transformations algébriques ou analytiques connues (fonctions puissances, exponentielles, logarithmiques,…), pourvu que le nouveau modèle reste interprétable. Cela peut permettre d’améliorer l’adéquation du modèle ou de diminuer son nombre de termes si on utilise ensuite une procédure de choix de modèles.

Changement discontinu de modèle • Test de Chow Le test de Chow permet prendre en compte un éventuel changement de structure dans l’écriture du modèle (en cela ce test porte plutôt pour des modèles d’évolution temporelle). Il s’agit donc de tester :

H0 : Y = X θ + ε contre H1 : Y (1) = X(1) θ1 + ε(1) et Y (2) = X(2) θ2 + ε(1).
On voit que sous H0 on a un sous-modèle de H1, alors que le modèle sous H1 peut aussi s’écrire comme un modèle linéaire avec Y = (Y (1)0,Y (2)0)0, Z = (X(1),X(2)) et θ0 = (θ0 1,θ00 2). On peut donc définir un test de Fisher de sous-modèle et on a, sous H0: b F = 1 k 1 n−2k SC0 −SC1 SC1 L −→ n→∞ 1 k χ2(k).

Hétéroscédasticité

Diagnostic d’héteroscédasticité

On représente également lesb Yi en fonction desb εi.
Table 1: Table des changements de variable pour la variable à expliquer Dans ce cas la variance des résidus semble inhomogène, puisque lesb εi ont une dispersion de plus en plus importante au fur et à mesure que les b Yi croissent. Un changement de variable pour Y pourrait être une solution envisageable pour “rendre” constante la variance du bruit (voir un peu plus bas). Remarque : certaines options sophistiquées utilisent plutôt des résidus réduits (Studentised residuals) qui sont ces mêmes résidus divisés par un estimateur de leur écart-type (généralement l’écart-type empirique) : cela donne une information supplémentaire sur la distribution des résidus qui doit suivre alors (toujours sous les postulats P1-4) une loi de Student. Cependant, on perd en capacité d’interprétation car le résidu est « adimensionnel », il n’est plus exprimé dans les unités de départ. Supposons par exemple que l’on veuille modéliser la taille (stature) d’adultes mesurée en mm. Un résidu de 5 correspond a une erreur de 5mm ce qui est tout-à-fait négligeable en pratique. Un résidu réduit est le plus souvent entre −2 et 2 (domaine de variation de la loi normale) sa valeur n’est pas directement interprétable.

Modifications possibles à apporter au modèle :

On ne peut envisager de transformer Y, que si les graphiques font suspecter une hétéroscédasticité. Dans ce cas, cette transformation doit obéir à des règles précises basées sur la relation suspectée entre l’écart-type résiduel σ et la réponse Y : c’est ce que précise le Tableau 3.2. Souvent ces situations correspondent à des modèles précis. Par exemple, la cinquième transformation correspond le plus souvent à des données de comptage. Dans le cas où les effectifs observés sont faibles (de l’ordre de la dizaine), on aura plutôt intérêt à utiliser un modèle plus précis basé sur des lois binomiales. Il s’agit alors d’un modèle linéaire généralisé. D’ailleurs toutes les situations issues d’une des transformations ci-dessus peuvent être traitées par modèle linéaire généralisé.

Il n’entre pas dans le champ de ce cours de préciser ces modèles (on pourra consulter par exemple le livre de McCullagh et Nelder).Notons cependant que pour des grands échantillons la transformation de Y peut suffire à transformer le modèle en un modèle linéaire classique et est beaucoup plus simple à mettre en œuvre. Par exemple, dans une étude bactériologique sur des désinfectants dentaires, on a mesuré le degré d’infection d’une racine dentaire en comptant les germes au microscope électronique. Sur les dents infectées, le nombre de germes est élevé et variable. L’écart-type est proportionnel à la racine carrée de la réponse. Une loi ayant cette propriété est la loi de Poisson, qui donne alors lieu à un modèle linéaire généralisé. Toutefois, si les décomptes sont en nombre important, travailler directement avec pour donnée la racine carrée du nombre de germe peut répondre tout aussi bien à la question.

Transformation de Box-Cox Lorsque les Yi sont des variables positives, on peut également utiliser une transformation continue de la variable Y sous la forme suivante: τ(Yi,λ) :=( Y λ i −1 λ pour λ 6= 0log Yi pour λ = 0 où λ est un réel a priori inconnu. Numériquement, on peut à partir d’une grille de valeurs de λ calculer la variance des résidusb σ2 b ε,λ pour chaque valeur de λ. On choisira alors: b λ = Argminλ∈[λmax,λmax]b σ2 b ε,λ.
Diagnostic de non-indépendance du bruit Un graphe pertinent pour s’assurer de l’indépendance des résidus entre eux et celui des résidus estimés b εi en fonction de l’ordre des données (lorsque celui-ci a un sens, en particulier s’il représente le temps).Un graphique comme celui ci-dessus est potentiellement suspect car les résidus ont tendance à rester par paquets lorsqu’ils se trouvent d’un côté ou de l’autre de 0. On pourra confirmer ces doutes en faisant un test de runs. Ce test est basé sur le nombre de runs, c’est-à-dire sur le nombre de paquets de résidus consécutifs de même signe. Sur le graphique ci-dessus, il y a 8 runs.

On trouve les références de ce test dans tout ouvrage de tests non-paramétriques ou dans un livre comme celui de Draper et Smith. Voir également un exercice. Par ailleurs, si les erreurs sont corrélées suivant certaines conditions (par exemple si ce sont des processus ARMA), il est tout d’abord possible d’obtenir encore des résultats quand à l’estimation des paramètres, mais il existe également des méthodes de correction (on peut penser par exemple à des estimations par moindres carrés généralisés ou pseudo-généralisés; voir par exemple les livres d’Amemiya, Green, Guyon ou Jobson).