Cours 4D Les graphes de Kiviat ou graphes radars, tutoriel apprendre les bases du langage 4D document PDF.
Nous pouvons à présent commencer le dessin proprement dit. Nous dessinerons dans l’ordre afin de respecter les effets de superposition :
– Les lignes de niveau du fond (formant une sorte de toile d’araignée)
– Le polygone des valeurs
– Les axes
– L’échelle
– Les noms des axes
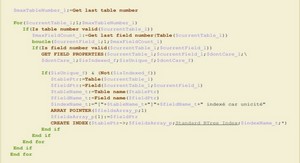
Le dessin des lignes de niveau utilise la fonction ch_Tableau vers polygone de 4D Chart permettant de dessiner un polygone défini par ses sommets.
Chaque valeur sera affichée sur un axe incliné d’un certain angle par rapport à l’horizontale. Cet angle dépend du nombre d’axes à dessiner. Cette série d’angles va servir un certain nombre de fois dans les calculs, il nous semble donc judicieux de les stocker temporairement dans un tableau dédié. Ceci présente l’avantage de
réduire le code et de simplifier la maintenance si nous désirons faire évoluer le calcul des angles.
Ici se pose le problème du sens horaire et du sens trigonométrique pour le calcul des angles.
Dans 4D, les fonctions trigonométriques utilisent des angles définis en radians ; elles sont basées sur le cercle trigonométrique qui « tourne » dans le sens anti-horaire. Par contre les habitudes pour le dessin des graphes de Kiviat (comme pour les diagrammes en secteurs) veulent que l’on respecte le sens de lecture usuel c’est-à dire en tournant dans le sens horaire. Nous devons donc en tenir compte pour calculer notre série d’angles ordonnée. De plus la lecture commence en haut du cercle (à 12 heures) alors que le cercle trigonométrique commence à droite (à 3 heures). Nous devons donc décaler d’autant nos angles.
Dans le code, nous utilisons la constante Degré qui permet de convertir facilement une valeur en degré vers une valeur en radians.
Voici le calcul des angles du graphe.
…….
Cours 4D Les graphes de Kiviat ou graphes radars (204 KO) (Cours PDF)