Corrigé du DM de statistiques

Corrigé du DM de Statistiques

Exercice 1

1. On s’intéresse à la proportion de chacune des intentions de vote. Nous allons donc utiliser la formule permettant de calculer l’intervalle de confiance d’une proportion dans la population.

Choix de la formule

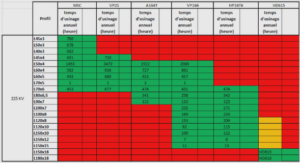
Nous avons à faire à un tirage sans remise mais avec un taux de sondage inférieur à 5% (1000 personnes < 5 % des votants). et sont et . Nous utilisons donc la formule suivante : b. Détermination du Le seuil de confiance est calculé à partir de la valeur de . Or donc Cette valeur peut être trouvée à partir d’une table de la loi normale centrée réduite ou à partir d’Excel. • Chercher la valeur qui se rapproche le plus de 0.025 dans la table de z et prendre la valeur de z correspondante. • Demander loi.standard.inverse dans Excel avec p=.025 Nous trouvons comme valeur 1,96. c. Calcul de l’intervalle de confiance des votes de l’UMP On prend comme estimateur ponctuel la proportion sur l’échantillon : Le pourcentage de voix en faveur de l’UMP sera situé entre 16,85% et 21,75% avec un seuil de confiance de 5%. d. Calcul de l’intervalle de confiance des votes du PS On prend comme estimateur ponctuel la proportion sur l’échantillon : Le pourcentage de voix en faveur du PS sera situé entre 15,14% et 19,86% avec un seuil de confiance de 5%. e. Calcul de l’intervalle de confiance des votes du FN On prend comme estimateur ponctuel la proportion sur l’échantillon : Le pourcentage de voix en faveur du FN sera situé entre 11,76% et 16,04% avec un seuil de confiance de 5%. 2. Pronostics Si on se réfère aux intervalles de confiance, l’UMP sera au deuxième tour. L’incertitude demeure, par contre entre le FN et le PS (limite supérieure du FN supérieure à la limite inférieure du PS).

Exercice 2 0. Distribution du QI dans la population

Echantillon de 250 lycéens parmi 3000

Estimation ponctuelle : L’estimation ponctuelle sur la population considérée est égale à la moyenne des QI sur l’échantillon, soit 115 ( ). Choix des formules à utiliser : Il s’agit d’un tirage sans remise avec un taux de sondage de 6,7% (>5%). Nous utilisons donc le coefficient d’exhaustivité ( ). L’effectif est supérieur à 30, donc nous utilisons la loi normale ( ).
Calculs : E = 3,5605

La « moyenne du QI » est la moyenne du QI sur l’ensemble des 3000 lycéens.
Comparaison d’une moyenne à une norme
i. H0 : . La moyenne du QI des lycéens provenant de l’établissement étudiés est égale à la moyenne du QI de la population globale, c’est à dire 100.
H1 : . La moyenne du QI dans le lycée étudié est supérieure à la moyenne du QI de la population globale (il était possible également de poser )
iii. Tirage sans remise, variance inconnue, n>30
iv. Il était possible éventuellement de calculer avec
vi. Si on rejette H0, sinon on rejette H1