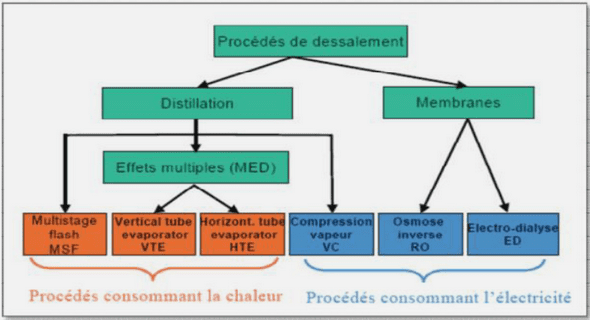
CONTRIBUTION DE LA SUCCION A LA DEFORMATION D’UNE STRUCTURE

Concepts de base de la dynamique des structures

D’une manière générale, la notion de structure s’attache à tout solide tridimensionnel caractérisé par une longueur L, une largeur l et une hauteur h. Les expressions des lois qui gèrent la dynamique des structures sont établies sur la base de la formulation des variations de l’état d’équilibre mécanique, sous l’action de contraintes internes ou externes qui sont appliquées. Cet état peut être marqué par des déformations ou des fissurations localisées qui seront traduites en terme de déplacement local des points constituant le milieu. En admettant l’hypothèse de faibles variations d’état et de la réversibilité des déformations, les lois qui gèrent la dynamique des structures sont établies selon la théorie de l’élasticité linéaire [39], [40]. Pour mener l’étude, la structure est associée à un ensemble de variables de description qui sont groupées dans ce qu’on appelle « configuration C(t) ». 

Configuration C(t)

Considérons un solide (Ω) quelconque, défini à tout instant t par son volume V(t) et sa surface frontière S(t), dans l’espace tridimensionnel rapporté à un système d’axes orthonormés (0, 𝑖,𝑗, 𝑘). En notant 𝑋, les coordonnées (x,y,z) d’un point P quelconque de (Ω), la configuration notée 𝐶(𝑋,𝑡) associée à (Ω) est définie par les variables suivantes : – les vecteurs position 𝑋(𝑡), vitesse 𝑋̇(𝑋,𝑡) et accélération 𝑋̈(𝑋,𝑡), – la masse volumique 𝜌(𝑋,𝑡), – les contraintes 𝜎(𝑋,𝑡), – les forces par unité de volume 𝑓𝑣(𝑋,𝑡), – les forces par unité de surface 𝑓𝑠(𝑋,𝑡). Soit, schématiquement : Figure IV. 1: Configuration C(t) d’un solide (𝜴) à un instant t 

Les grandeurs de description

Une description macroscopique de la déformation des structures peut être établie en utilisant le concept de la configuration C(t), selon le formalisme suivant : toute contrainte initiale exercée en un point P quelconque de (Ω) provoque le déplacement du point et, par la suite, la déformation du solide ; cette déformation instaure un nouveau champ de contrainte et, les faits se succèdent d’une manière cyclique jusqu’à l’obtention d’un nouvel état d’équilibre. Selon ce formalisme, on peut dégager trois grandeurs de description qui sont : le vecteur déplacement noté 𝑈, le tenseur de déformation (𝜀) et le tenseur de contrainte (𝜎). 𝒌 𝒋 𝒊 P 𝜌(𝑡) 𝑋(𝑡), 𝑋̇(𝑡), 𝑋̈(𝑡) 𝜎(𝑡) 𝑓𝑣 (𝑡), 𝑓𝑠 (𝑡) Volume V(t) Surface S(t) (𝛀) 𝑥 𝑦 𝑧 85 Laboratoire de Physique et Modélisation IV.1.2.1- Vecteur déplacement et tenseur de déformation Sous l’action d’une force appliquée pendant un intervalle de temps [𝑡0,𝑡], chaque point du solide (Ω) se déplace. Considérons alors un segment de longueur 𝛿 dans(Ω) tel que : – à un instant initial 𝑡0 , le segment est positionné par [𝑃 0𝑅 0 ], de longueur 𝑑𝑋 0 , dans la configuration 𝐶 0 (𝑋 0 ,𝑡) associée à (Ω) – à un instant ultérieur 𝑡 = 𝑡0 + ∆𝑡, le segment est positionné par [𝑃𝑅], de longueur dX, dans la configuration 𝐶(𝑋,𝑡) associée à (Ω) (Figure IV.2). Figure IV. 2: Schématisation du déplacement d’un segment de (𝜴) Selon ce schéma, le passage du segment [𝑃 0𝑅 0 ] à par [𝑃𝑅] peut être interprété comme résultant de deux mouvements successifs : – un mouvement de translation généré par le vecteur 𝑈 =< 𝑢 𝑣 𝑤 >, ramenant [𝑃 0𝑅 0 ] en [𝑃𝑅 ′ ] – un mouvement de rotation d’angle 𝜃 autour de P, ramenant le segment [𝑃𝑅 ′ ] en [𝑃𝑅] Dans cette représentation schématique,  𝑈 désigne le vecteur déplacement du point 𝑃 0  𝑈 + 𝑑𝑈 désigne le vecteur déplacement du point 𝑅 0  𝑑𝑈 = 𝑑𝑋 − 𝑑𝑋 0 représente le vecteur déformation de (Ω) traduit sur le segment [𝑃 0𝑅 0 ] .