CONCEPTION D’UN CODE DE TRANSPORT SOLIDE POUR LES COLLECTEURS D’ASSAINISSEMENT

L’objectif de notre code <MEDCA> : Modélisation de l’Evolution de Dépôt en Collecteur d’Assainissement, est de simuler l’évolution du profil de dépôt ainsi que sa composition dans le temps et dans l’espace. Nous synthétisons les principes de sa conception ci-dessous : Le transport solide est dominé par le charriage : <MEDCA> est un code de charriage. La suspension est entièrement ignorée. Les solides transportés, quelles que soient leurs tailles, restent toujours dans la couche de charriage à la proximité du fond.  Les solides dans le dépôt et ceux transportés ont de tailles très variables. Ceci provoque des phénomènes de dépôt spécifiques et particuliers (aggravation granulométrique dans le temps et forte dégradation granulométrique dans l’espace, phénomènes de masquage et de pavage). Afin de les bien simuler, il est indispensable de considérer l’influence de cette granulométrie étendue ainsi que certains traitement spécifiques liés à celle-ci sont exigés; Comment traiter la configuration géométrique d’une canalisation, autrement dit, comment considérer ses sections transversales et sa configuration longitudinale, ceci est le premier problème fondamental rencontré dans la modélisation de l’hydraulique. La forme géométrique de la section n’influence pas seulement les paramètres hydrauliques, la distribution hétérogène des contraintes de cisaillement du fond dans le sens transversal (Viswanathan & Leutheusser 1970), mais aussi le transport solide notamment le transport solide par charriage (Ackers et al. 1977, Kleijwegt 1992).

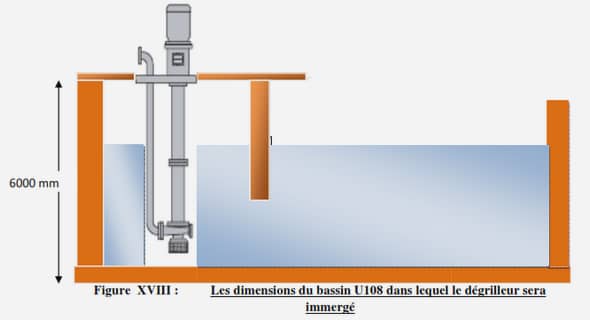
Presque tous les codes classiques font l’hypothèse d’un canal rectangulaire. Ce traitement fausse plus ou moins les résultats et les collecteurs de réseaux d’assainissement étant de petites dimensions par rapport à celles de cours d’eau naturels, l’influence de la géométrie sur le transport solide en collecteur est certainement plus importante qu’en rivière. De plus, il est également difficile de trouver un code de transport solide qui tienne compte de l’influence des virages. Ceci ne permet pas de reproduire les phénomènes exacts de dépôt, notamment les virages de forte courbure qui peuvent créent des phénomènes vraiment particuliers (voir chapitre 6).  Nous avons donc décidé de considérer la configuration géométrique réelle du collecteur 13 de Marseille. Par contre, la présence des ondulations du lit, ainsi que les problèmes induits par celle-ci (Raudkivi 1964), sont ignorés dans notre étude. L’écoulement par temps sec dans le collecteur 13 est quasiment permanent et stable par période dans la journée (chapitre 2, figure 1.4-1), aussi notre code <MEDCA> traite-il le régime hydraulique comme permanent Da ns ce cas, le modèle de la ligne d’eau, construit au chapitre 5 pour l’étude de la perte d’énergie des écoulements de temps sec du collecteur 13, peut être utilisé pour chaque période quotidienne caracté­ristique.

Il est à noter que celui-ci peut être obtenu à partir du système du modèle complet de transport solide général (équations {9-2} et {9-3}) par les simplifications suivantes: 1/ L’écoulement est permanent; 2/ La présence des solides transportés n’est pas prise en compte dans l’hydraulique lorsque leur quantité est assez faible. Le dépôt présente un phénomène de forte aggravation de la granulométrie dans le temps et de forte dégradation de celle-ci de l’amont vers l’aval du tronçon (figure 2.4-1). Ceci est également vrai pour les solides transportés au sein de l’écoulement Un seul diamètre représentatif n’est évidemment pas suffisant pour simuler ce phénomène de tri granulométrique, et il convient de prendre en compte l’ensemble de la granulométrie.  Selon l’analyse du paragraphe 9.7, il est difficile déjuger si les fractions découpées représentent correctement l’ensemble de la granulométrie. Mais, du moins, le mode de découpage et le nombre de fractions découpées doivent permettre à <MEDCA> de bien reproduire les phénomènes réels, et sont justifiés par les résultats du code. q’s,Íép. Suivant le critère du choix des formules décrit dans le chapitre 8, nous avons retenu la formule d’Ackers-White (équation {10-2} à {10-5}) et la formule de Meyer-Peter (équation {10-6}) modifiée avec condition critique x.cr = 0.036 pour le calcul de g¡¡,7* » (Note: les résultats de calcul présentés dans la quatrième partie ont été obtenus éventuellement avec cette dernière). La formule de Wang (équation {10-8}) a été sélectionnée pour le calcul de la valeur q’sbaip.