La modélisation de bassin

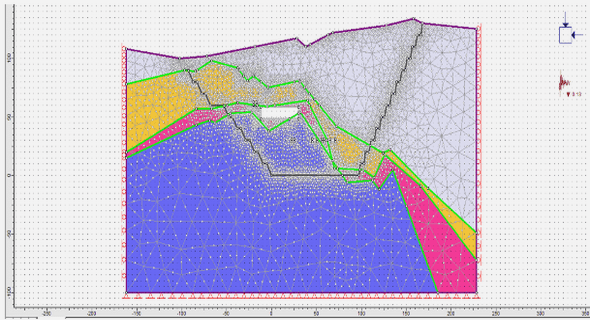
La modélisation de bassin a pour but de simuler l’ensemble des processus physiques qui vont de la génération des hydrocarbures à partir des roches mères, à la migration, et à l’accumulation dans les zones réservoirs. Cette modélisation est utilisée par les plus grandes compagnies pétrolières en exploration. L’expérience acquise tout au long des nombreuses études menées montre que la compréhension du système pétrolier est très souvent un phénomène 3D. Un modèle en 3D est nécessaire pour représenter la géométrie à l’âge actuel et sa reconstruction dans le passé, puis pour prédire les chemins de migration, et en dernier point, pour estimer les volumes en place. Des outils logiciels de modélisation de bassin existent déjà en 3D mais pour des structures complexes où les failles sont représentées simplement. Des outils existent aussi en 2D avec des structures complexes faillées. Les structures complexes plissées faillées en 3D restent encore un sujet de recherche en modélisation de bassin car de nombreux problèmes restent à résoudre. Concernant le problème de la restauration 3D, il existe des outils surfaciques et volumiques. Le couplage simulation des transferts de fluides et restauration est encore difficile dans le cas de modèles de bassin 3D complexes. 

Le problème 

Comment modéliser les transferts de fluide dans les bassins sédimentaires ? Plusieurs facteurs entrent en ligne de compte : • l’évolution de la géométrie et la cinématique des failles présentes dans le bassin, • l’évolution des propriétés de transfert le long des failles et entre les couches sédimentaires, • l’évolution de la déformation des écailles avec différents mécanismes de déformation. La géométrie des failles est importante pour la caractérisation et les contraintes que l’on applique au cours de la cinématique d’un bassin. Si on arrive à qualifier l’ensemble des failles présentes sur un bassin sédimentaire, une première idée de la cinématique du bassin peut-être envisagée. La surface de faille est définie comme la surface de glissement entre deux blocs. Les failles peuvent être principalement de trois types (Fig. 1.1) : • les failles normales ont un plan de faille incliné vers le bloc affaissé (le phénomène lié est une extension horizontale, Fig. 1.1 (a)), • les failles inverses ont un plan de faille qui surplombe le bloc affaissé (le phénomène lié est la compression horizontale ce qui correspond à une faille chevauchante, Fig. 1.1 (b)), • les failles décrochantes correspondent à un plan de faille vertical sur lequel se produit un glissement horizontal (Fig. 1.1 (c)). Les failles peuvent avoir des histoires complexes suivant les événements qui surviennent sur un même bassin sédimentaire au cours des temps géologiques. Le comportement rhéologique des roches peut induire différents comportements cassant ou ductile. Ainsi, les séismes peuvent induire des circulations de fluides par fracturation. Mais ils peuvent également induire des processus de compaction qui vont cicatriser ces fractures et réduire les circulations. La géométrie des failles et la cinématique des blocs constituant les bassins impliquent la déformation des écailles. Des plis peuvent alors apparaître. Les roches constituant les différentes couches géologiques peuvent avoir des comportements rhéologiques différents. Ces comportements impliquent des modes de déformation différents. Deux modes de déformation sont considérés dans le cas de contact parfait (sans frottement), la flexion et le cisaillement vertical. D’autres phénomènes physiques interviennent dans la géométrie actuelle de nombreux bassins sédimentaires : • la sédimentation accumule des dépôts suivant des agents dynamiques externes comme l’eau et le vent ou par des processus physico-chimique, • l’érosion est responsable de l’évolution des reliefs engendrés par la déformation de l’écorce terrestre, • la compaction tasse les roches meubles constituant les bassins sédimentaires au cours du temps. Cette présentation très générale des phénomènes géologiques amène beaucoup de questions. Comment comprendre et modéliser l’ensemble de ces phénomènes physiques ? Dans cette thèse, l’accent est mis spécifiquement sur la cinématique des bassins 3D complexes et sur la caractérisation de la surface de faille qui est une surface de glissement. L’essentiel de la thèse se développe autour du processus de déformation du bassin après dépôt et compaction. Les processus d’érosion ne sont pas encore intégrés dans les modèles.

L’existant et ses limites

Les modèles cinématiques 2D

 Les modèles qui vont suivre décrivent la cinématique des plis sur des rampes en deux dimensions (2D). Le prototype développé dans la thèse s’inspire de ces différentes méthodes. 

Modèle de SUPPE

Ce modèle est la première tentative d’approche cinématique 2D et il sert de base à beaucoup d’autres modèles. Le modèle de SUPPE ([15], 1983) traite des plis à déplacement parallèle en coupe et les relations angulaires associées au déplacement de ce pli par rapport à la rampe. Le mécanisme définissant ce déplacement a pour base le plissement par flexion pour des couches infiniment stratifiées. Le déplacement du compartiment chevauchant sur la rampe est supposé parfait, c’est à dire sans frottement et la transformation est supposée isopaque (c’est à dire que les couches de la coupe stratigraphique ne varient pas d’épaisseur au cours du déplacement). Par ailleurs la roche, constituant le modèle, est supposée incompressible ce qui implique une condition supplémentaire qui est la conservation des aires. Le modèle est basé sur deux principaux éléments : • le positionnement des « kinks » aux zones charnières du bassin, • la résolution d’une équation trigonométrique du troisième degré reliant les angles du chevauchement et l’angle de la rampe (Fig. 1.2, équation 1.1) : tan θ tan γ(1−tan2 γ+2 tan γ tan τ ) = (tan τ (1−tan2 γ)−2 tan γ)(tan γ−2 tan θ) où : • les données du problème sont : – θ est l’angle entre la direction de la stratification dans l’écaille et le support de celle-ci, avant pliage sur le kink, – φ est l’angle entre les deux directions du support, de part et d’autre du point de rupture de pente (c’est à dire le kink), • les inconnues sont : – β est l’angle entre la stratification dans le second compartiment et le support de celui-ci, après pliage sur le kink, – γ est l’angle entre la direction de la stratification et le kink

Modèle de CONTRERAS et SUTER 

 Le modèle de CONTRERAS et SUTER , est un précurseur dans l’application d’une méthodologie discrète de déformation d’un pli d’une rampe. Il présente un algorithme cinématique basé sur une description Lagrangienne pour un modèle direct. L’ensemble du domaine est subdivisé en domaine de pendage constant et de vecteur déplacement associé également constant (même direction de déplacement). Les différents domaines de pendage sont subdivisés au niveau des changements de pendage à l’aide des bissectrices, exemple la droite (DR2) (Fig. 1.4). Les différents vecteurs déplacement restent parallèles au support de glissement, ce qui se traduit par les relations suivantes si on reste dans un même domaine de déplacement..