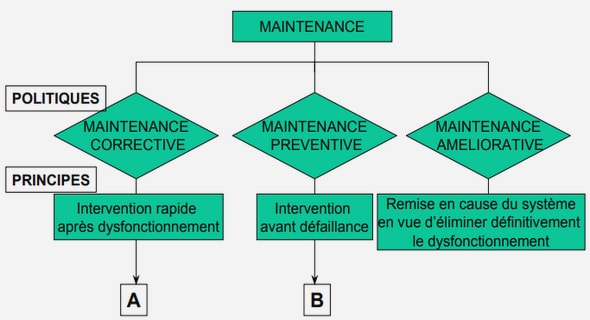
Test d’adéquation de la distribution stationnaire de la chaîne de Markov basé sur la divergence de Bregman

Chaînes de Markov à temps discret

Dénition et exemples Une chaîne de Markov est un réseau spécique de variables aléatoires décrit par un système dynamique d’états de transitions. Elle respecte les propriétés suivantes tirées de [25, 31]. Soient S un ensemble ni ou dénombrable et X0, X1, X2, . . . une suite de variables aléatoires à valeurs dans S. La notation X indique le processus stochastique correspondant et P sa loi. Dénition 1.1. On dit que X est une chaîne de Markov si pour tout n ∈ N, et pour tout x0, x1, . . . , xn+1 ∈ S telle que P(X0 = x0, X1 = x1, . . . , Xn = xn) > 0, P(Xn+1 = xn+1 | Xn = xn, Xn−1 = xn−1, . . . X0 = x0) = P(Xn+1 = xn+1 | Xn = xn). (1.1) S est appelé espace des états de la chaîne. Remarque 1.1.1. La condition de Markov peut aussi s’écrire pour tout m, n ∈ N et {xi , i ∈ N} à valeurs dans S, sous la forme : P(Xm+n = xm+n | Xm = xm, Xm−1 = xm−1, . . . , X0 = x0) = P(Xm+n = xm+n | Xm = xm)(1.2) Test d’adéquation de la distributions . . . c Dieudonné NIYITANGA/201507CYF/Option: Prob & Stat/FST/UCAD 2018 Chaînes de Markov à temps discret : Dénition et exemples 3 Ainsi, on peut dire d’un processus X qu’il est markovien si son état actuel fourni toute l’information nécessaire pour connaître son évolution future. Sa distribution dans le futur étant donné le présent et le passé ne dépend que du présent. On parle alors d’absence de mémoire. Dénition 1.2. (Homogénéité) Une chaîne de Markov est dite homogène lorsque la probabilité de transition (1.2) ne dépend pas de n, c’est à dire : P(Xn+1 = j | Xn = i) = P(X1 = j | X0 = i), ∀n ∈ N et ∀i, j ∈ S. (1.3) L’homogénéité d’une chaîne de Markov précise donc que la probabilité de passer de l’état i à l’état j reste la même à travers le temps c’est-à-dire le mècanisme de transition ne change pas au cours du temps. Ainsi, elle permet de condenser dans une seule matrice les probabilités de transitions entre deux états quelconques. La dénition 1.2 permet alors de caractériser une chaîne de Markov homogène à l’aide d’une matrice de transition et d’un vecteur d’états initiaux. Dénition 1.3. Soit X = {Xn}n∈N une chaîne de Markov d’espace d’états S. Soient (i, j) ∈ S2 deux états. On appelle la probabilité de transition de l’état i à l’état j la quantité : pij = P(Xn+1 = j | Xn = i) = P(X1 = j | X0 = i), ∀n ∈ N. (1.4) Dénition 1.4. On appelle matrice de transition de la chaîne de Markov X toute matrice P vérie les propriétés suivantes : 1. Encadrement des coecients : 0 6 pij 6 1 ∀i, j ∈ S. (1.5) 2. Somme par ligne : X j∈S pij = 1 ∀i, j ∈ S. (1.6) 3. Spectre : P admet la valeur propre 1, le vecteur e = [1, . . . , 1]0 étant un vecteur propre associé. La matrice carrée P indexée par S est dite stochastique ou markovienne si ses élèments pij satisfont les deux propriétés (1.5) et (1.6). Si P est une matrice stochastique, alors toutes ses puissances P 2 , P3 , . . . sont encore des matrices stochastiques. Dénition 1.5. On appelle matrice doublement stochastique une matrice stochastique P telle que tP soit aussi stochastique. Exemple 1.1. Le cas le plus simple est 2 × 2 (un espace à deux états). Sans perte de généralité, on peut penser que les états sont 0 et 1 : alors les entrées seront pij i, j = 0, 1. Ici, la matrice stochastique a la forme : P =   1 − a a b 1 − b   avec 0 6 a, b 6 1. En particulier, a = b = 0 donne la la matrice identité ou matrice unité I et a = b = 1 la matrice anti-diagonale. 

Exemple 1.4. Un modèle simple de prévision météo

: Soit Xn une variable aléatoire indicatrice qui indique si elle va pleuvoir le jour n. L’ensemble d’index est T = {0, 1, 2, . . .} c’est discret et représente vraiment le temps dans ce cas on suppose que chaque jour, il y a deux états possibles : de la pluie ou pas de pluie. D’oú on dene l’ensemble des états  0, il pleut; 1, il ne pleut pas. Soit {0, 1} qui est aussi discret. On suppose que le fait qu’il pleuve demain (ou non) depend seulement du fait qu’il pleuve (ou non) aujourd’hui uniquement c’est-à-dire pas de conditions météorologiques précédentes (Propriété de Markov). Soit α la probabilité qu’il pleuve demain, étant donné qu’il pleut aujourd’hui. Soit β la probabilité qu’il pleuve demain, étant donné qu’il ne pleut pas aujourd’hui. 

Classication des états 

Il existe diérents types d’états. Leur classication permet de mieux étudier les propriétés asymptotiques des chaînes de Markov. Maintenant, classions les états possibles selon diverses caractéristiqués. 1.2.1 Caractères récurrents et transitoires Les dénitions qui suivent sont tirés des ouvrages [8, 16, 21, 23, 25]. Dénition 1.7. Soit i ∈ S où S est l’espace des états. 1. Un état i est dit récurrent si, P(∃n > 1, Xn = i | X0 = i) = 1. C’est-à-dire que la probabilité d’un éventuel retour à l’état i vaut 1, sachant que la chaîne a commencé à l’état i. Sinon, on dit que l’état est transitoire ; 2. Un état i est dit récurrent positif si le temps moyen de récurrence dans l’état i, ρi = E[Ti | X0 = 1] avec Ti = min{n > 1 : Xn = i} où Ti = ∞ si Xn > 1 ∀n > 1 [25], est ni pour tout i ∈ S. Sinon, l’état i est dit récurrent nul