Bases de la modélisation en mécanique des fluides
Une présentation moins succinte de ces bases, en ce qui concerne toutes celles-ci exceptées la loi de comportement des fluides compressibles (section 1.5) et le bilan d’énergie interne (section 1.9), est accessible dans mon document de cours de première année Plaut (2015b). Par rapport `a ce cours « élémentaire », on donne aussi en plus ici section 1.6 quelques compléments sur la physique de la viscosité. Vous noterez qu’un plan de ce cours de deuxième année est donné ci-après, naturellement, a la fin de la section 1.5.
Modèle du milieu continu fluide, liquide ou gaz
Ce modèle, introduit dans la section 1.1 de Plaut (2015b), suppose que la matière est constituée de « particules matérielles » ou « volumes élémentaires représentatifs » de diamètre caractéristique d dans un état local homogène de quasi-équilibre thermodynamique, suffisamment gros pour contenir suffisamment d’atomes ou de molécules pour que cette notion de quasi-équilibre ait un sens du point de vue de la physique statistique, d’échelle des hétérogénéités atomiques ou moléculaires, (1.1) suffisamment petits pour qu’ils méritent le titre de « particules », d L échelle des hétérogénéités « macroscopiques » ‘ 1 cm. (1.2) Dans le cas de liquides « simples », `
Cinématique
On retrace ici les grandes lignes des sections 1.2, 2.1 et 2.2 de Plaut (2015b).
Descriptions du mouvement
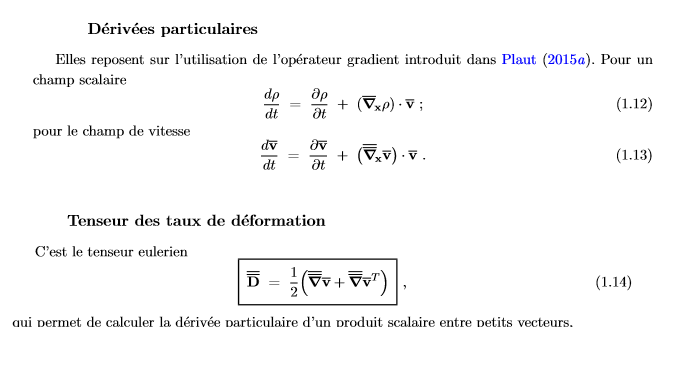
Si le modèle du milieu continu est valable on peut définir la vitesse v(x,t) d’une particule matérielle comme une quantité moyenne (au sens de la physique statistique). D’ou le champ de vitesse eulerien ; la description lagrangienne du mouvement Φ(.,t) : D0 domaine initialement occupé −→ Dt domaine actuellement occupé X position initiale 7−→ x position actuelle = Φ(X,t) (1.9)
En mécanique des fluides on utilisera de préférence la description eulerienne; ainsi le champ de vitesse par exemple v = v(x,t) .