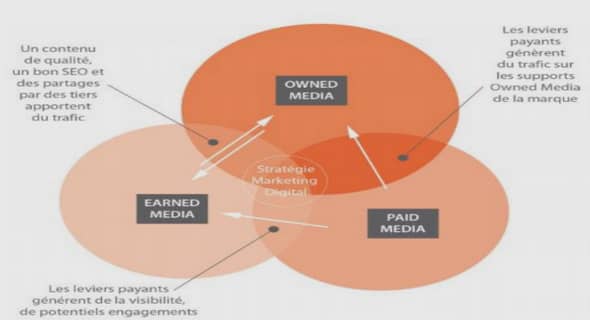
Autocalibration d’antenne vibrante ou déformée
Modélisation des enregistrements
Le capteur électromagnétique
Le choix d’un capteur électromagnétique se fait essentiellement en fonction de l’application souhaitée. Dans le cadre de l’écoute, les antennes doivent pouvoir couvrir une grande bande de fréquences (plusieurs octaves). Toujours dans un soucis de performance en écoute, leur diagramme d’antenne doit être le plus omnidirectionnel possible afin de surveiller la plus grande surface possible. Enfin, les antennes ne doivent pas être trop volumineuses pour qu’elles puissent être facilement intégrées à l’aéronef. Pour des fréquences inférieures à 1 GHz, il est difficile de trouver des antennes capables de satisfaire tous ces points. Le plus critique est en fait la taille de l’antenne (type fouet ou sabre) qui peut ne pas être en adéquation avec les contraintes aéronautiques. Au delà du GHz, le type d’antennes est plus diversifié : spirale, hélice, patch. Les antennes spirales peuvent avoir un diagramme de rayonnement quasi omnidirectionnel. Le diamètre de la spirale est généralement de l’ordre d’une demi-longueur d’onde de la fréquence la plus basse, ainsi, ce type d’antenne peut être plaqué sur la surface de l’aéronef. Si l’on connaît précisément la gamme de fréquences à écouter, on peut utiliser des capteurs bande-étroite comme par exemple les antennes patch. Ces capteurs sont les plus utilisés en aéronautique car ils permettent de créer des antennes dites conformes (capteurs qui sont de plus de faible poids et souvent peu coûteux).
Modélisation des enregistrements
Dans la suite du document, on supposera que les différents capteurs composant l’antenne sont omnidirectionnels et identiques, c’est à dire que tous les capteurs possèdent la même réponse en fréquence, ceci quelle que soit la direction d’arrivée de l’onde. On supposera enfin que les capteurs sont suffisamment éloignés les uns des autres de façon à pouvoir négliger les problèmes éventuels de couplages électromagnétiques.
Modélisation d’une contribution en bande de base
Influences du milieu de propagation et des capteurs
On considère que le milieu, bien que susceptible de modifier le signal au cours de la propagation, reste non sélectif en fréquence (non filtrant) dans le voisinage du réseau. Cette hypothèse est réaliste dans la mesure où les émissions captées sont bande-étroite et que la taille globale de l’antenne (la distance entre les deux éléments les plus éloignés) n’excède pas une dizaine de mètres. Les capteurs étant supposés omnidirectionnels et identiques, un signal source donné sera reçu sur les différents capteurs à une même transformation près avec différents retards de propagation. Ces signaux seront appelés les contributions sur porteuse du signal source sur les différents capteurs du réseau. On se place dans un cas idéal non bruité où une unique source j cohérente est reçue (on parle de système SIMO : Single Input, Multiple Output). Si Ri(t) représente le signal reçu sur un capteur i, on écrira d’après (1.1) la contribution de la source j sur ce capteur selon Ri(t) = Re n gs f j (t − τ 0 ij ) exp(2πfp(t − τ 0 ij ))o . Le paramètre τ 0 ij est le temps de propagation de l’onde depuis la source j jusqu’au capteur i. Le signal s f j (t) correspond au signal source modifié à la fois par le milieu de propagation, par la fonction de transfert du capteur et par l’électronique de la chaîne de réception. g est le gain statique de la chaîne. Il est toujours possible de choisir arbitrairement un capteur de référence (par exemple le capteur numéro 1) pour lequel on posera R1(t) = Re n gs f j (t − τ 0 1j ) exp(2πfp(t − τ 0 1j ))o = Re{C1j (t)}. (1.2) C1j (t) est la contribution complexe de référence. Au niveau d’un capteur i quel12 Chapitre1 conque, on peut exprimer le signal reçu en fonction de C1j (t) et écrire successivement Ri(t) = Re n gs f j (t − τ 0 ij ) exp(2πfp(t − τ 0 ij ))o = Re n gs f j (t − τ 0 1j − (τ 0 ij − τ 0 1j )) exp(2πfp(t − τ 0 1j − (τ 0 ij − τ 0 1j )))o (1.3) = Re{C1j (t − τij )}. τij , τ 0 ij − τ 0 1j correspond au retard de propagation relatif de la source j depuis le capteur de référence jusqu’au capteur i. En supposant que le retard de propagation relatif τij est toujours très petit devant le temps de cohérence 1 2B du signal source sj (t) et la largeur de bande 2B étant par ailleurs très petite devant la fréquence porteuse fp (émission bande-étroite), nous pouvons considérer que l’effet de la propagation n’affecte sensiblement que le terme relatif à la porteuse dans l’expression de la contribution retardée (1.3). En d’autres termes, en considérant que s f j (t−τ 0 1j −τij ) ≈ s f j (t−τ 0 1j ), il vient, d’après (1.2) et (1.3), pour l’expression de la contribution sur porteuse de la source j sur le capteur i : Ri(t) ≈ Re{C1j (t) exp(−2πfpτij )}. (1.4)
Effets de la chaîne d’acquisition
La localisation de sources se faisant par des traitements numériques, on doit procéder à l’acquisition des signaux captés Ri(t). Dans ces applications, on ne cherche pas à démoduler les sources, mais à estimer les phases relatives des ondes porteuses au niveau des différentes antennes du réseau. Plusieurs techniques sont alors envisageables pour effectuer l’acquisition indirecte de ces mesures. Nous considèrerons la numérisation suivante adaptée aux antennes bande-étroite. Les signaux captés Ri(t) sont préalablement ramenés en bande de base en effectuant un changement de fréquence au moyen de deux oscillateurs locaux en quadrature de phase généralement calés sur la fréquence correspondant au milieu de la bande du capteur. La partie basse-fréquence des signaux obtenus est numérisée en utilisant une période d’échantillonnage Te. On obtient selon (1.4), après filtrage passe-bas de la sortie du premier mélangeur et après numérisation, le signal numérique r P i [kTe] = r P i [k] = Re{c1j [k] exp(−2πfpτij )}. c1j [k] est la contribution en bande de base de la source j sur le capteur de référence. Dans le cas particulier où l’oscillateur local délivre, en synchronisme, une fréquence égale à celle de la porteuse, nous aurons directement c1j [k] = gs f j (kTe − τ 0 1j ). Sur le second mélangeur en quadrature avec le premier, nous obtiendrons, de façon équivalente après filtrage passe-bas et numérisation, le signal : r Q i [k] = Im{c1j [k] exp(−2πfpτij )}. On peut construire le signal complexe ri [k] = r P i [k] + r Q i [k] = exp(−2πfpτij )c1j [k]. (1.5) Le signal complexe en bande de base reçu sur un capteur i quelconque du réseau correspond donc au signal reçu par le capteur de référence à un terme d’amplitude complexe près dépendant du retard de propagation relatif de la source et donc de la position du capteur considéré. C’est sur ce signal que seront effectués les traitements liés à l’autocalibration.
Introduction |