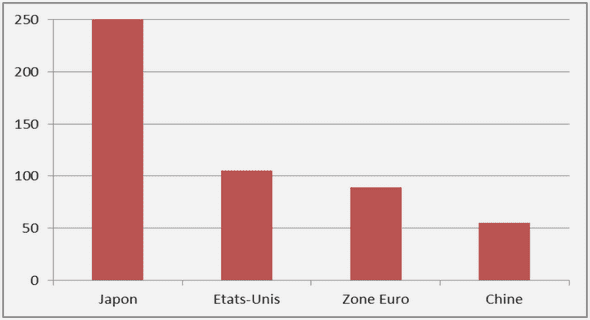
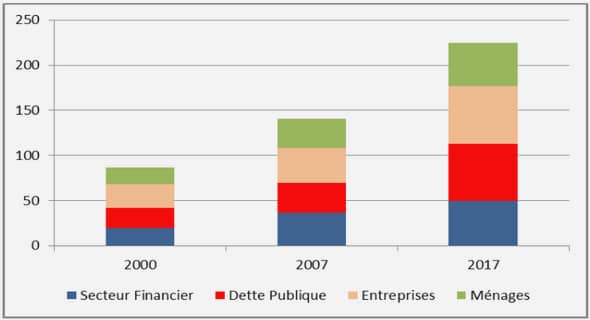
Approche par variables d’état

Ces modèles supposent que l’histoire passée n’intervient que par la valeur ac­ tuelle d’un certain nombre de variables, les variables d’état, dont l’évolution est régie par une équation d’évolution [Sidoroff, 1975a]. Dans ce groupe, on réunit les modèles basés sur une approche par potentiels à l’image des travaux de We­ ber [Weber, 1968] et de Sidoroff [Sidoroff, 1976] ainsi que les principaux modèles rhéologiques tels que le modèle de Maxwell ou celui de Burger. Les modèles rhéologiques que l’on va décrire ci-dessous correspondent à des matériaux viscoélastiques solides ou liquides. On peut trouver leur description dans [Germain, 1973], [Eringen, 1967], [Mandel, 1977]. Ces modèles sont obtenus en combinant des ressorts et des amortisseurs, permettant ainsi de donner une interprétation des différentes variables d’état apparaissant dans le modèle. On cherchera, à chaque fois, à choisir convenablement les variables d’état et on dé­ finira les potentiels d’énergie libre $ et de dissipation <f>. Le comportement d’un matériau est entièrement décrit par les variables d’état x — i^iX •>  » ‘ ? X ) et les  Il est décrit par deux variables d’état, la déformation linéarisée totale (s) et une déformation irréversible £. qui peut être vue comme la déformation d’un amortisseur fictif contenu dans le matériau (figure 2.1). Remarque 2.1 La notation tensorielle précédente est à prendre avec précaution. Dans le cas tridimensionnel’, si le matériau est isotrope, on fait une décomposi­ tion des tenseurs en une partie volumétrique et une partie déviatorique. S’il est anisotrope¡ on se place dans les axes principaux. Cette loi est l’écriture classique (en particulier pour un traitement numérique) de la loi de comportement des matériaux viscoélastiques de Maxwell. Elle per­ met de prédire le comportement des matériaux de Maxwell soit en relaxation (évolution de la contrainte de traction en fonction du temps pour une elongation imposée) soit en fluage (évolution de la déformation en fonction du temps pour une contrainte imposée) (figure 2.2). On remarque un fluage infini, ce qui montre qu’un tel matériau se comporte comme un fluide.

Le modèle de Burger généralisé

On peut donc prédire le comportement en relaxation et en fluage pour de tels matériaux (figure 2.4). Dans ce cas, le fluage est limité ce qui montre que ce type de matériau se comporte comme un solide avec deux temps de relaxation différents. Ces modèles rhéologiques ont l’inconvénient d’être limités aux cas des petites déformations en raison de la décomposition additive des différentes grandeurs constitutives.  Weber [Weber, 1974] décrit les comportements viscoélastiques (ou viscoplas- tiques) par l’expression d’une énergie libre ^ en fonction de la température, du tenseur de Cauchy-Green droit C et de variables d’état xi» X’¿  » • * XN- H effectue les hypothèses suivantes:  Weber décompose le gradient de transformation F en une partie élastique Fe et une partie anélastique F° (detFa = 1) qui permet de passer de la confi­ guration de référence à la configuration relâchée (voir Sidoroff [Sidoroff, 1974], [Sidoroff, 1975a], [Sidoroff, 1975a], [Sidoroff, 1976]). L’hypothèse d’isotropie des configurations relâchées conduit à identifier le tenseur x à Fa • *Fa = Ça . où C est une fonction isotrope de A ou du tenseur de contrainte de Cauchy q_ à valeurs positives ou nulles. Si C est strictement positive, alors le comporte­ ment ainsi défini est celui d’un fluide viscoélastique, sinon, c’est celui d’un solide viscoplastique au sens de Weber (viscoélastique sans élasticité instantanée).

D’autre part, le comportement identifié par les relations (1.42) et (1.43) est conforme au principe d’objectivité, au second principe de la thermodynamique et au principe d’Onsager et est invariant dans tout changement de configuration de référence, à condition que le volume soit constant. Les limitations d’un tel modèle viennent du fait que le choix d’une seule variable d’état tensorielle peut s’avérer insuffisante pour la représentation des matériaux visqueux, et ce, au même titre que les modèles à un seul état intermé­ diaire. Sidoroff [Sidoroff, 1974] développe la notion d’état intermédiaire à partir de laquelle il construit une classe de milieux viscoélastiques non linéaires. Ces mo­ dèles généralisent aux grandes déformations les modèles rhéologiques classiques (Maxwell, Kelvin…). La configuration intermédiaire est définie comme une confi­ guration relâchée, obtenue par une relaxation instantanée des contraintes, ce qui n’a de sens que pour les milieux à élasticité instantanée. Conformément à la  théorie des grandes déformations, il introduit, comme variable d’état, la défor­ mation anélastique Fa (ou la déformation élastique Fe), et décompose le gradient de transformation sous forme multiplicative (figure 2.6): F = Fe • Fa .