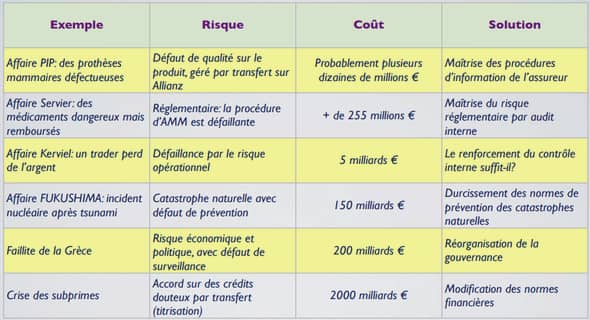
Le principe de comparaison

Le principe de comparaison, applelé aussi méthode des sous-solutions et sur-solutions, est une méthode très utile et largement utilisée dans la recherche des solutions de problèmes de réaction diffusion. Cette méthode permet d’étudier l’existence, l’unicité, la stabilité, l’explosion en temps fini et le comportement asymptotique des solutions. On l’utilise en général sur une classe spécifique de systèmes de réaction-diffusion quasimonotone. Ce principe utilise en grande partie les résultats du principe du maximum fort, qui dit que si u et v sont deux solutions telles que u ≤ v sur le bord du domaine ∂Ω, alors u ≤ v dans Ω. Considérons l’équation parabolique suivante :

Sous-solutions et Sur-solutions du problème elliptique associé

Les solutions elliptiques représentent les solutions d’équilibre qui ne dépendent pas du temps. Elles sont souvent décrites comme des états asymptotiques atteints par des solutions de problèmes paraboliques dépendant du temps. Ces solutions de problèmes elliptiques obéissent au principe du maximum, voir [83]. Dans ce paragraphe, nous allons décrire la méthode itérative de sous-solutions et sur-solutions qui nous permettra dans la suite d’étudier l’existence et la stabilité des solutions issues de problèmes elliptiques. Nous considérons alors le problème elliptique suivant.

Généralité sur les ondes progressives

En 1937, Kolmogorov et al [52], ont émis l’idée que les ondes progressives peuvent être décrite non seulement par les équations hyperboliques mais aussi par des équations paraboliques non linéaires. Dans les années soixante-dix, sous l’influence d’un grand nombre des problèmes les plus divers de physique, chimie et biologie, un développement intensif de ce thème a commencé. Le nombre considérable de problèmes sciences mentionnés ci dessus, conduisent à des solutions de type onde progressive et sont modélisé par un système d’équations paraboliques de la forme où u = (u 1 , …, um) est une fonction à valeur vectorielle qui représente la dynamiques des espèce en temps et en l’espace, D est une matrice symétrique définie positive représentant les coefficient de diffusion, ∆ est l’opérateur de Laplace, et F (u) une fontion vectorielle à valeur vectorielle décrivant l’interaction locale entre les espèces. Les solution du système (1.4.26) sont définies dans un domaine Ω de l’espace R n dont la frontière ne coïncide pas celle de R n et leurs conditions aux limites sont spécifiées suivant le l’origine du problème.
Nous allons d’abord donner des exemples d’ondes progressives. Ensuite, suivant la forme de la fonction F (u) nous presentons des méthodes classiques pour prouver le théorème d’existence.

Quelques exemples d’ondes progressives

Les ondes progressives décrites par des systèmes paraboliques peuvent être divisés en plusieurs classes. L’exemple le plus classique est celui des ondes dites stationnaire qui sont les solutions du système (1.4.26) u(x, t) = w(x 1 − ct, x ′ ), où w(x) est une fonction de n variables, x = (x 1 , …, x n ), x = (x 2 , …, x n ), et c est une constante qui représente la vitesse d’onde. Nous supposons ici que Ω est un cylindre, et que le système de coordonnés est choisi de manière que l’axe x1 est dirigée dans l’axe du cylindre.
Au cours des dernières années un vaste ensemble un certain nombre de modèles mathématiques ont été étudiés dans laquelle non seulement des ondes stationnaires peuvent être observées, mais aussi des périodiques. En particulier, nous pouvons observer des ondespériodiques, définies comme des solutions u(x, t) du système (1.4.26) de la forme,

Solutions exactes de fronts avec une réaction polynomiale

Méthode de factorisation

La méthode de factorisation est une technique bien connue utilisée pour trouver des solutions d’ODE. Cela remonte aux travaux de Schrödinger dans les quelles il a résolu certains exemples de l’équation portant son nom [79], et elle a été ensuite développé par Infeld et Hull [45] pour trouver des solutions analytiques de certaines classes d’équations différentielles de second ordre. Dans un contexte plus général, la factorisation a déjà été introduite dans [78, 16] pour des équations différentielles ordinaires de la forme.

Étude du modèle proie-prédateur avec diffusion

La biologie et l’écologie sont de fait, des sciences descriptives. La description est un premier pas vers la compréhension d’un système. Cependant, une telle première étape doit être accompagnée par le développement d’un cadre théorique en vue de parvenir à une réelle idée et de pouvoir faire un prédiction chaque fois que cela est possible. Les écologistes ou biologistes sont de plus en plus confrontés aux défis de prévoir les conséquences des changements des systèmes qu’ils observent. Par exemple, nous devons mieux comprendre comment la biodiversité marine diminue à mesure qu’une espèce de poisson est pêchée au delà, ou comment traiter une tumeur à un stade avancé de façon à minimiser les effets secondaires des médicaments. C’est à cette fin que la théorie vient se greffer à ces champs expérimentaux.
Ce chapitre décrit une étude théorique d’un modèle proie-prédateur. Cette étude peut être appliquée à la prédiction de la dynamique d’espèces d’un écosystème. Il s’agit de déterminer comment il s’auto-organise pour produire des structures spatiales complexes.
L’auto-organisation de ces structures ou ”patterns” spatio-temporels est un des fascinants résultats qui a été découvert ces dernières années. Ce sont par exemple les structures de Turing, les Spiral waves, le chaos spatio-temporel ou encore les ”finger prints”, voir [100].

Introduction

En ne tenant pas en compte la dimension spatiale, le modèle que nous considérons est de type proie-prédateur. Les interactions locales sont définies de façon à ce que la population de proie suit une croissance logistique tandis que la réponse fonctionnelle du prédateur à la proie est de la forme Holling type II. Le modèle qui découle de ces interactions locales est le suivant.

Existence de travelling wave solutions

Les ”travelling waves” ou ondes vogageuses sont des bifurcations globales que l’on peut observer dans la nature ou de façon expérimentale, ou même encore dans certains modèles de problèmes d’évolution. Ce sont en fait des solutions du problème considéré qui connectent deux états d’équilibre. L’existence de ces solutions a été conjecturée par Fisherdans [34] et Kolmogorov dans [52] a donné la preuve de leur existence. Dans sa thèse en 1980, pour construire ces travelling waves, Dunbar dans [29] a développé une méthode assez générale et applicable sur les modèles proie-prédateur avec diffusion. En 2007, les auteurs de [2] ont donné une méthode applicable sur des modèles qui ne sont pas de type proie-prédateur. Cette méthode n’utilise que les outils de l’analyse fonctionnelle. En fait dans ce paragaphe nous allons développer les mêmes arguments que les auteurs de l’article [2] pour construire une telle solution qui va connecter deux équilibres homogènes. Donc la méthode que l’on va utiliser est uniquement basée sur la théorie de l’analyse fonctionnelle et elle peut être appliquée à des modèles proie-prédateur en général.

Chaos spatio-temporel

Les systèmes biologiques sont en général hors d’état d’équilibre. Les systèmes s’autoorganisent en brisant la symétrie des instabilités. Ainsi des structures telles que les spiral waves, les black eyes ou encore d’autres motifs spatiaux sont observés dans un large éventail de systèmes chimiques et biologiques, voir [62, 64, 70, 98, 100] pour plus de détails. Ces motifs sont les fluctuations de la distribution spatiale et sont une découverte majeure de ces deux dernières décennies. Cependant un défi sera de comprendre et de prédire leur formation sachant qu’ils sont étroitement liés aux interactions non linéaires et complexes du système étudié. On observe une distribution spatiale de type onde spirale pour le système (2.2.4), voir figure 2.9. Le chaos spatio-temporel est un autre type de motif dans lequel les densités changent de façon apériodique en espace et en temps, comme dans la turbulence. Ces structures et ces phénomènes spatio-temporels sont émergents et résultent de causes très simples, dans le sens où ce sont des motifs macroscopiques obtenus à partir d’un simple couplage d’interaction et la régle de diffusion locale. En d’autres termes, ils ne sont pas programmés dans les équations, voir [11, 47, 69, 70].
Dans ce sous-paragraphe, nous étudions le problème (2.2.4) dans le domaine Ω = [0, 900] × [0, 900] de R 2 , le flux est nul sur le bord de Ω. Nous nous intéressons aux structures émergentes pour le système (2.2.4). Remarquons que si (u ∗ , v ∗ ) est un équilibre instable pour le système (2.2.3) alors il l’est aussi pour le système (2.2.4) dès que les deux espèces ontle même coefficient de diffusion. Ainsi les paramètres sont fixés de telle sorte que (u ∗ , v ∗ ) est instable pour (2.2.3). On suppose aussi que les deux espèces diffusent de la même façon, c’est à dire δ = 1. La condition initiale est une légère perturbation au voisinage de l’équilibre (u ∗ , v ∗ ) ayant une faible disparité de la répartition spatiale.

Analyse qualitative de la dynamique d’une chaîne alimentaire de trois espèces

Introduction

Une des méthodes généralement utilisée en biologie ou en écologie dans le processus de conservation et du contrôle de la dynamique des espèces, est l’introduction d’une population supplémentaire appelée “super-prédateur”. Cependant l’impacte de cette introduction doit, au préalable, faire l’objet d’une étude afin de réduire au minimum les effets indésirables.
La modélisation mathématique apporte une solution raisonnable à cette étape. Alors, nous considérons un modèle de réaction-diffusion avec trois espèces. Le terme de diffusion décrit la capacité à mouvoir dans un domaine Ω de R n , n = 1, 2, 3, que nous supposons fermé. Le flux au bord de ce domaine est supposé nul. La première population notée U1 est l’unique source de nourriture de la deuxième U2 . De même le prédateur U2 (espèce intermédiaire ) est l’unique proie du super-prédateur U3 . Les interactions locales entre les espèces U1 et U2 sont modélisées par un schéma de type Lotka-Volterra, alors que celles entre U2 et U3 sontde type Holling type II. En absence de diffusion le modèle s’écrit de la façon suivante.

Non existence de solutions stationnaires

Nous allons montrer que sous certains paramètres, le problème (3.1.2) n’admet aucun équilibre positif. Ceci implique que les populations de proie, de prédateurs et de superprédateurs ne peuvent exister que sous ces conditions. Nous avons besoin au préalable d’énoncer le lemme suivant de [28] que nous utiliserons dans la suite.

Formation des motifs

Les hétérogénéités spatiales ou spatio-temporelles sont une des caractéristiques de nombreux systèmes écologiques et épidémiologiques et ont de profonds effets sur la dynamique d’invasion, la croissance et la persistance des populations (voir [56]). Ces hétérogénéités sont des facteurs déterminant de l’auto-organisation du système étudié. L’identification des facteurs et paramètres permettant de passer de l’état homogène stable à l’émergence de motifs spatiaux ou spatio-temporel est une question d’une grande importance dans l’étude des processus biologiques ou dans la compréhension de l’évolution des écosystèmes. Dans ce paragraphe nous allons donner pour ce modèle de trois espèces, les conditions permettant la formation de structures non-homogènes puis nous allons illustrer par la simulationnumérique ces prédictions mathématiques.

Approche combinée utilisant les adénovirus réplicatifs pour la thérapie génique du cancer

Introduction

Près de trente années de recherches intensives et plus de 1,2 million de publications traitant du cancer ont permis l’accumulation d’une grande quantité d’informations quant à la genèse de cette maladie. Des résultats tant sur l’analyse d’altérations génomiques chez l’humain que sur l’expérimentation en culture cellulaire et chez l’animal ont clairementétabli que le développement du cancer est le résultat d’une combinaison entre, d’une part, l’activation de voies favorisant la prolifération cellulaire et, d’autre part, l’inhibition de signaux restreignant le potentiel prolifératif des cellules. Hanahan et Weinberg [41] ont récemment proposé de classifier ces différentes modifications en six catégories, qui semblent généralement retrouvées dans chaque type de cancer : autosuffisance en signaux de croissance, insensibilité aux signaux d’inhibition de croissance, résistance à l’apoptose, potentiel réplicatif infini, potentiel de néovascularisation et capacité d’invasion tissulaire.
Nous allons présenter un état des lieux des nouveaux outils de thérapie en cours de développement qui tirent directement leurs bases stratégiques des découvertes moléculaires de la transformation cellulaire. Les traitements traditionnels du cancer, telles la chimiothérapie et la radiothérapie, ont pour principal défaut une absence de sélectivité entre cellules saines et cellules transformées. Une thérapie qui ciblerait sélectivement les cellules cancéreuses sans affecter les tissus sains avoisinants serait évidemment un grand progrès. La mise en évidence des enchaînements moléculaires pouvant entraîner un cancer a parallèlement offert autant de nouvelles cibles potentielles pour espérer bloquer la maladie.
L’activité antitumorale est le fait de l’action simultanée du cycle viral lytique et d’un ou de plusieurs gènes thérapeutiques. La connaissance de la biologie des virus et de leurs interactions avec les protéines du cycle cellulaire ont permis de développer des virus oncolytiques ayant un meilleur ratio efficacité/toxicité. Ces virus sont appelés virus réplicatifs conditionnels ou sélectifs car à cause de leurs modifications génomiques et structurelles, ils se répliquent préférentiellement dans les cellules tumorales. Cette propriété peut être intrinsèque au virus lui même, comme par exemple la transformation cellulaire par activation du proto-oncogène « Ras », ce qui permet la réplication virale et entraîne la destruction des cellules infectées. Les études réalisées in vivo dans différents modèles murins de tumorigenèses, ont révélé que l’infection locale par les réovirus entraîne la régression des tumeurs.
De tels virus oncolytiques pourraient donc représenter une voie thérapeutique de certains cancers, voir [93].
Ce chapitre traite d’une procédure de thérapies combinées contre le cancer en utilisant les virus oncolytiques et les inhibiteurs. Les adénovirus sont des virus icosaédriques non enveloppés à ADN double brin. Ils sont très étudiés dans le but d’une application possible en thérapie génique ou en thérapie anticancéreuse. La réplication des adénovirus génétiquement modifiés infectent les cellules cancéreuses, se reproduisent à l’intérieur d’eux et éventuellement, causent leur mort. Quand les cellules infectées meurent, les virus à l’intérieur d’eux sont libérés et infectent ensuite d’autres cellules tumorales.
Il est connu depuis 1976 que les adénovirus humains du sous-groupe C et les coxsackievirus du groupe B ont un récepteur en commun, voir [60]. En 1997, la nature de ce récepteur a été déterminée , il est appelé CAR (coxsackie-adenovirus receptor) [15]. La protéine CAR est une protéine transmembranaire de type 1 appartenant à la famille des immunoglobulines (Ig). Cette protéine de 46 kDa est ubiquitaire à la surface des tissus cellulaires humains et elle est constituée d’un domaine intracellulaire et d’un domaine extracellulaire séparés par un domaine transmembranaire. Le succès de la prolifération du virus dans les cellules cancéreuses est lié à la présence du récepteur CAR.
Nous allons introduire des terminologies de biologistes que nous utiliseront dans ce chapitre et qui ne sont pas familières à un mathématicien. ONYX-015 est un adénovirus génétiquement modifié, conçu sélectivement pour se répliquer et selyser dans des cellules cancéreuses tout en épargnant les cellules normales.
Les voies de signalisation : Les cellules perçoivent les changements de leur environnement par l’intermédiaire de récepteurs, le plus souvent membranaires. Ces récepteurs vont transmettre un signal extracellulaire à l’intérieur de la cellule en activant une série de modifications protéiques ou une cascade de signalisation qui va permettre à la cellule de réagir. Les voies de signalisation des inhibiteurs MEK (Mitogen Activated Protein Kinase), permettent l’engagement rapide d’un programme d’expression génique en réponse à un stimulus. Ces voies de signalisation ont été extrêmement bien conservées au cours de l’évolution et sont constituées de protéines kinases qui s’activent en cascade et transmettent le signal par une suite d’interaction entre protéines. Les voies de signalisation des MEK, comme celles de p38 ( voir [93]), jouent un rôle important dans le contrôle de la mort cellulaire. Toutefois, les inhibiteurs MEK temporaires peuvent provoquer l’arrêt du cycle cellulaire qui inhibe le cycle de vie de ONYX-015 (voir [99, 101]).

Table des matières

Introduction générale 
1 Préliminaires
1.1 Le principe de comparaison
1.2 Existence locale
1.3 Sous-solutions et Sur-solutions du problème elliptique associé
1.4 Généralité sur les ondes progressives
1.4.1 Quelques exemples d’ondes progressives
1.5 Solutions exactes de fronts avec une réaction polynomiale
1.5.1 Méthode de factorisation
2 Étude du modèle proie-prédateur avec diffusion 
2.1 Introduction
2.2 Existence globale et bornage des solutions
2.2.1 Existence et bornage des solutions
2.2.2 Existence d’états d’équilibre
2.3 Stabilité des états équilibres
2.3.1 Stabilité locale des états d’équilibres
2.3.2 Stabilité globale de l’équilibre homogène non trivial
2.4 Existence de travelling wave solutions
2.4.1 Préliminaires
2.4.2 Construction de la solution travelling wave
2.5 Dynamiques complexes et la formation de patterns spatio-temporels
2.5.1 Étude de bifurcations locales en dimension spatiale égale à un
2.5.2 Les instabilités de Turing et de Hopf
2.5.3 Chaos spatio-temporel
3 Analyse qualitative de la dynamique d’une chaîne alimentaire de trois espèces 
3.1 Introduction
3.2 Existence globale des solutions
3.3 Analyse des solutions stationnaires
3.3.1 Existence de solutions stationnaires
3.3.2 Non existence de solutions stationnaires
3.3.3 Stabilité locale des solutions stationnaires homogènes
3.3.4 Stabilité globale de l’équilibre endémique homogène
3.4 Formation des motifs
3.4.1 Étude théorique de l’ »instabilité de diffusion »
3.4.2 Applications
4 Approche combinée utilisant les adénovirus réplicatifs pour la thérapie génique du cancer 
4.1 Introduction
4.2 Modélisation du problème
4.3 Étude mathématique du modèle
4.4 Simulation numérique
A.1 Espaces de Sobolev
A.1.1 Définition et propriétés
A.1.2 Inégalités de Sobolev
A.2 Les espaces de Hölder
A.3 Le critère de Routh-Hurwitz
B.1 Méthode Spectrale : Exemple simple
B.2 La méthode Pseudo-Spectrale
B.2.1 L’équation de Schrödinger avec potentiel
B.3 Transformées rapides et équations non-linéaires
B.3.1 La Transformée de Fourier Rapide
B.4 Les méthodes (pseudo)-spectrales et le calcul des dérivées d’une fonction