La Valeur Critique
La valeur critique ou p-value est la probabilité qu’une suite produite par un générateur parfait ait l’air moins aléatoire que la suite examinée par le test. Cette valeur dépend de la forme de l’hypothèse alternative (Ha). Si la p-value a alors l’hypothèse nulle est acceptée et dans le cas contraire elle est rejetée.
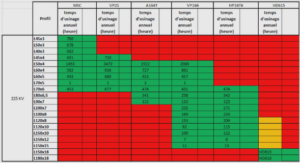
Cependant la validation de l’hypothèse nulle est basée sur une p-value > a mais également sur l’uniformité réparties dans l’intervalle [a, 1] des valeurs des p-values > a. Voici la répartition en 2 parties des 15 tests du NIST :
Test de fréquence Monobit
Définition 4.2.1. Le test de fréquence Monobit est un test qui détermine si le nombre de uns et de zéro dans une séquence est approximativement le même que celui prévu pour une séquence véritablement aléatoire. Pour ce faire on commence toujours par convertir les uns et les zéro de la séquence d’entrée en valeur de 1 et 1 grâce à la formule xi = (2ui 1).
Test de Rang d’une Matrice Binaire
Définition 4.2.2. Le test sur le rang de la matrice binaire est un test qui permet de calculer le rang des sous-matrices disjointes issues de la séquence entière.
Ce test à pour but de vérifier la dépendance linéaire entre les sous-chaînes de longueurs fixes de la séquence d’origine.
Cependant le choix ne se porte pas sur la longueur du bloc, mais sur celle des lignes.
Le principe qui suit nous montre que les séquences aléatoires passent avec succés ce test.
Test de Run
Définition 4.2.3. Le test de Run est un test qui permet de déterminer le nombre total de séquence de bits identiques ininterrompue dans une séquence entière.
Ce test permet aussi de déterminer si le nombre de run de uns et de zèro de différentes lon-gueurs est approximativement le même que celui prévu pour une séquence aléatoire. Pour ce faire, on calcul d’abord avant le test la proportion p de uns de la séquence d’entrée
Test Universel de Maurer
Définition 4.2.4. Le test de Maurer est un test qui permet de déterminer le nombre de bits entre deux modèles identiques.
Le but de ce test est de détecter si la séquence peut être compressée de manière significative sans perte d’information et toute séquence nettement compressible est considérée comme non aléa-toire.
Le principe qui suit nous montre que les séquences aléatoires passent avec succés ce test.
Principe 4.2.4. Soit Un une suite de taille n ; L la longueur de chaque bloc et Q le nombre de blocs dans la séquence d’initialisation.
Test de Transformée de Fourier Discrète (Spectrale)
Définition 4.2.5. Le test de transformée de fourier discrète (spectrale) est un test qui permet de déterminer les hauteurs maximales de la séquence.
Le but de ce test consiste à détecter les caractéristiques de périodicité de la séquence d’origine. Autrement dit ce test permet de vérifier si le nombre de pics (N1) dépassant le seuil q (T = (log 0.105 ) n) de 95% est significativement différent de 5%.
Le principe suivant nous montre que les séquences aléatoires passent avec succés ce test.
Test de Correspondance des Modèles Sans Chevauchement
Définition 4.2.6. Le test de correspondance des modèles sans chevauchement est un test qui permet de déterminer le nombre d’occurences des modèles pré-spécifiées.
Le but de ce test consiste à détecter les générateurs qui produisent trop d’occurences pour un modèle non périodique donné.
Ce test utilise une fenêtre à m bits pour rechercher le motif spécifique (B) correspondant.
Si B n’est pas trouvé, la fenêtre glisse d’une position de bit et dans le cas contraire la fenêtre est réinitialisée sur le bit après le motif trouvé et la recherche reprend.
Le principe suivant nous montre que les séquences aléatoires passent avec succés ce test.