Stabililsation

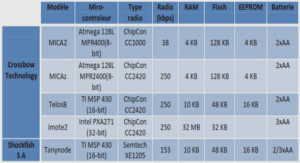
Stabililsation

Ce chapitre s’intéresse à la stabilisation des éléments finis par la méthode SUPG (pour Streamline Upwind Petrov-Galerkin) [24] que le code AeTher utilise. Cette méthode de stabilisation consiste en la modification des fonctions test, afin de décentrer la discrétisation des termes d’advection. Si l’on note LAdv : V 7→ Ae iV,i l’opérateur des flux d’Euler et L : V 7→ Ae iV,i +  Ke ijV,j ,i l’opérateur des équations de Navier-Stokes stationnaires, alors la contribution d’un élément Ω e à la forme faible stabilisée est : Z Ωe (W + τLAdvW) T · (LV) dΩe . (5.1) La matrice τ , dite de stabilisation, est d’une importance capitale pour la méthode. Elle est définie aux éléments et doit être symétrique et définie positive. La valeur de ses coefficients règle la viscosité numérique introduite dans le calcul. Il existe plusieurs façons de construire la matrice τ . Dans AeTher, cette matrice est construite de manière algébrique, en utilisant les propriétés des opérateurs de convection exprimés en variables entropiques. Cette construction, proposée par Mallet [104], est expliquée en détail dans la première section de ce chapitre. Ce n’est pas la seule méthode pour construire τ . Par exemple, Le Beau introduit dans [16] une matrice de stabilisation diagonale, multiple de l’identité. Le coefficient scalaire est proportionnel à un rapport de longueur de l’élément sur le rayon spectral de l’opérateur de flux d’Euler. Une définition similaire est proposée dans [78]. On pourra consulter [89] pour un panorama complet des formes du paramètre τ en 1D. La formulation SUPG peut s’interpréter de multiples manières. Hughes et al. expliquent le lien fort entre l’erreur commise à une petite échelle et la stabilisation SUPG dans [80], qui permet de s’interroger sur le bien-fondé d’une matrice de stabilisation constante sur chaque élément. Par exemple, Knobloch dans [95] propose une définition du  paramètre τ utilisant les informations des éléments voisins. La deuxième section de ce chapitre est consacré à l’essai d’une matrice τ qui est construite sans approximations sur la formule proposée dans [83, 104]. 5.1 Forme de la matrice de stabilisation La stabilisation des équations de Navier-Stokes par la méthode SUPG exige de bien définir la matrice de stabilisation τ . Cette section suit la présentation de Mallet dans [104] et permet de mieux comprendre la nécessité de la stabilisation des équations d’advection ainsi que la construction de cette matrice, dont la formule a été donnée dans la section 2.2.2 et est redonnée ici : τ = Ae −1 0 ∂ξi ∂xj ∂ξi ∂xk AjAk !− 1 2 , (5.2) où Ae 0 est la matrice de passage des variables entropiques vers les variables conservatives, Aj sont les matrices de flux d’Euler et ∂ξ ∂x est la jacobienne de passage des coordonnées vers celles de l’élément de référence. 5.1.1 Stabilisation d’une équation d’advection 1D Différence finie centrée et méthode upwind Soit le problème modèle d’advection-diffusion en une dimension suivant :    au,x − ku,xx = 0 sur ]0, L[ u(0) = g0 u(L) = gL (5.3) Ici, a > 0 représente la vitesse d’advection, et k le coefficient de diffusion. Ces deux grandeurs sont constantes sur tout le domaine. Ce problème admet une solution analytique qui dépend du nombre de Péclet P e = aL k : u(x) = c1 + c2 exp P e x L  (5.4) où c1,2 sont des constantes dépendant des conditions limites. On peut chercher une solution approchée à ce problème par des méthodes de différences finies. On découpe le domaine spatial en N éléments de longueur h, délimités par x0, x1, . . . , xN . On note ui ‘ u(xi) la discrétisation de u. Lemme 5.1. La discrétisation de l’équation d’advection-diffusion (5.3) par un schéma de différences finies centrées, utilisant comme approximation CHAPITRE 5. STABILISATION 113 discrète des dérivées spatiales    ui,x = ui+1 − ui−1 2h ui,xx = ui+1 − 2ui + ui−1 h 2 , (5.5) donne une solution oscillante si le nombre de Péclet local α = ah 2k est strictement supérieur à 1. Démonstration. La discrétisation du problème continu (5.3) par le schéma des différences finies centrées, dont les dérivées sont définies dans l’équation (5.5) est a ui+1 − ui−1 2h − k ui+1 − 2ui + ui−1 h 2 = 0 , (5.6) soit en regroupant les termes, et en divisant l’équation par k h2 pour faire apparaître α : ui+1(α − 1) + 2ui + ui−1(−α − 1) = 0 . (5.7) La suite (ui) a une solution de la forme ui = c−x i − + c+x i + , (5.8) où x− et x+ sont racines du polynôme caractéristique de l’équation de récurrence. Ces racines sont réelles et distinctes. Elles valent    x− = 1 x+ = 1 + α 1 − α . (5.9) La solution discrète ui s’exprime en fonction de constantes c1 et c2 dépendant des conditions limites : ui = c1 + c2  1 + α 1 − α i . (5.10) Si α > 1, le terme de croissance géométrique 1+α 1−α est négatif. La solution discrète va donc présenter des oscillations numériques. La méthode de différence finie décentrée (upwind) permet de s’affranchir de ces oscillations. La discrétisation décentrée du terme d’advection fait cette fois-ci uniquement intervenir le terme « au vent » de ui (d’où le nom anglais de upwind), qui est donc ui−1

Viscosité artificielle

Théorème 5.3. Il existe une viscosité artificielle ˜k, fonction de α et de h et vérifiant 0 < ˜k ≤ ah/2, qui rajoutée à la viscosité physique du problème d’advection-diffusion (5.3), permet d’obtenir la solution exacte aux nœuds lorsque ce nouveau problème est discrétisé par le schéma des différences finies centrées. Démonstration. L’équation d’advection-diffusion devient au,x −  k + ˜k  u,xx = 0 . (5.14) Si l’on pose le nouveau nombre de Péclet local α˜ = ah 2(k+k˜) , on obtient par un développement similaire la solution du schéma centré : ui = c1 + c2  1 + ˜α 1 − α˜ i . (5.15) On veut qu’il soit égal à la solution exacte, qui vaut u(xi) = c3 + c4 exp P exi L  . (5.16) De plus, xi = hi. Ainsi on doit avoir ∀i ∈ [1, N − 1], c1 + c2  1 + ˜α 1 − α˜ i = c3 + c4 exp(2iα) . (5.17) Nécessairement, c1 = c3 et c2 = c4. Ainsi  1 + ˜α 1 − α˜  = exp(2α) ⇐⇒ α˜ = e 2α − 1 e 2α + 1 Cela permet d’exprimer α˜ en fonction de α : α˜ = tanh(α). (5.18) Or, si l’on pose le nombre sans dimension ˜ξ = 2k˜ ah, α˜ s’écrit α˜ = 1 1 α + ˜ξ . (5.19) CHAPITRE 5. STABILISATION 116 α ˜ξ 1 1 3 Figure 5.2 – Fonction d’amortissement ˜ξ de la correction visqueuse en fonction du nombre de Péclet local α Ainsi, on obtient la définition suivante de la fonction ˜ξ, qui est également tracée sur la figure 5.2 : ˜ξ = coth α − 1 α . (5.20) En utilisant la relation ˜ξα = ˜k/k, la viscosité artificielle ˜k pour rendre le schéma exact aux nœuds vaut ˜k = kα˜ξ(α) . (5.21) La viscosité artificielle ˜k dépend donc de la viscosité physique, du nombre de Péclet local α et d’une fonction d’amortissement ˜ξ. Lorsque le nombre de Péclet α tend vers l’infini, ˜ξ(α) tend vers 1. La viscosité artificielle vaut alors kα = ah 2 , qui est bien le résultat trouvé pour les équations d’advection seules. On va retrouver cette formule dans le cas des éléments finis, abordé dans la section suivante. Méthode des éléments finis de Galerkin et de Petrov-Galerkin Dans cette partie, on cherche à appliquer les résultats précédents à la méthode des éléments finis. Des fonctions de forme de Lagrange P1 sont utilisées pour la discrétisation. On introduit l’espace discret V h : V h = n v ∈ C0 ([0, L]) , ∀ i, v|[xi,xi+1] ∈ P1([xi , xi+1])o , (5.22) où C 0 ([0;L]) désigne l’espace des fonctions continues de [0;L] dans R, et P1([xi , xi+1]) sont les fonctions linéaire de [xi , xi+1] dans R.  La solution discrète est cherchée dans l’espace V h a , sous-ensemble de V h dont les membres vérifient les conditions aux limites en 0 et en L demandées à la solution du problème (5.3) : V h a = n v ∈ Vh , v(0) = g0, v(L) = gL o , (5.23) L’espace affine V h a a un espace vectoriel associé, noté V h 0 dont les fonctions vérifient des conditions de Dirichlet homogènes au bord : V h 0 = n v ∈ Vh , v(0) = 0, v(L) = 0o . (5.24) Le problème d’advection-diffusion (5.3) discrétisé par des éléments finis de Lagrange P1, c’est-à-dire que la solution discrète u h est recherchée dans V h a et les fonctions de pondération w h appartiennent à V h 0 , s’écrit : ∀ w h ∈ Vh 0 , Z L 0 −w h ,xauh + w h ,xkuh ,xdx = 0 (5.25) Lemme 5.4. La discrétisation du problème d’advection-diffusion (5.3) par la méthode des éléments finis de Lagrange P1 (5.25) est identique à celle donnée par le schéma aux différences finies centrées Démonstration. Soit l’élément de référence le segment [−1, 1]. Les fonctions de formes sur l’élément de référence sont N1 = 1−x 2 et N2 = 1+x 2 . Soit un élément Ω e de longueur h. Calculons les matrices élémentaires de base sur cet élément : Mij = Z Ωe NiNjdx = Z Ωref NiNj h 2 dx , M = h 3 1 1 2 1 2 1 ! , Nij = Z Ωe Ni,xNjdx , N = 1 2 −1 −1 1 1 ! , Pij = Z Ωe Ni,xNj,xdx , P = 1 h 1 −1 −1 1 ! . La matrice élémentaire correspondant à la forme faible discrète (5.25) sera − aN + kP = a 2 + k h a 2 − k h − a 2 − k h − a 2 + k h ! . (5.26) On en déduit qu’après assemblage, la discrétisation pour h constant et égal à h sera après division par h ui−1  − a 2h − k h 2  + ui 2k h 2 + ui+1 a 2h − k h 2  = 0 . On reconnaît exactement la discrétisation par la méthode des différences finies centrées.