Modélisation de la Machine polyphasée à Pôles lisses
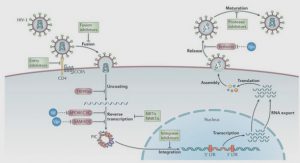
Géométrie et constitution des machines considérées Les machines considérées sont des machines radiales à aimants déposés. Dans cette section, la géométrie et les notations adoptées pour représenter la machine sont explicitées puis les propriétés magnétiques des aimants constituant les pôles sont détaillées.
Topologie
Les machines considérées sont des machines radiales à aimants déposés. Le rotor peut être interne ou externe. Les conducteurs de phase sont disposés dans des encoches statoriques de forme rectangulaire. La figure II.1 représente la géométrie d’encoche considérée ainsi que la structure générale de la machine. Les notations qui y sont précisées sont reprises dans le tableau II.1. Afin de faciliter la modélisation et le calcul du champ, comme dans le chapitre I, la machine est munie de deux repères de calcul : • un repère fixe lié au stator dont l’origine est positionné sur un axe de phase de la phase 0 ; ce repère est noté Rs(Os, −→er , −→et) • un repère tournant lié au rotor dont l’origine est positionné au centre d’un pôle ; ce repère est noté Rr(Or, −→er , −→et) Figure II.1 — Modélisation des encoches et spécification des notations Le décalage instantané entre les deux repères correspond à la position instantanée du rotor. Elle est notée θRr/Rs = θ. L’angle correspondant à la position d’un point P du stator dans le repère statorique est noté θP ∈S/Rs = θs. L’angle correspondant à la position d’un point P du rotor dans le repère rotorique est noté θP ∈R/Rr = θr.
Type d’aimants
Le rotor de la machine est constitué d’aimants déposés, ce qui signifie que les pôles ne sont pas saillants. La culasse rotorique est à géométrie cylindrique et les aimants sont calés en surface. Les aimants considérés sont magnétiquement rigides. Dans un domaine de fonctionnement stabilisé, une caractéristique linéaire relie induction et champ magnétique : −→B = µa −→H + −→M Dans cette expression, µa désigne la perméabilité de l’aimant et −→M est l’aimantation rémanente. Dans tout le volume d’aimant, la perméabilité est supposée constante et égale à la perméabilité de l’air : µa ≈ µ0 Cette hypothèse est tout à fait acceptable pour des aimants à champ coercitif élevé (tels que les ferrites ou les composés terres rares) o`u, généralement, µa vaut environ 1.1µ0. De même, l’aimantation rémanente maintient sa norme constante dans tout le volume d’aimant quelque soient les conditions d’utilisation. En d’autres termes, le modèle proposé ne tient pas compte des effets liés à la démagnétisation1 . Les aimants sont des matériaux a priori conducteurs. Donc ils peuvent être le siège de perte par courant de circulation. En effet, si la conductivité de l’aimant est notée σa, la loi d’Ohm relie le champ électrostatique −→E et la densité de courant −→j dans l’aimant : −→j = σa −→E Cependant, en régime permanent, l’induction vue par les aimants du rotor (qui résulte de la force magnétomotrice statorique) peut être considérée invariante en première approche. Donc le deuxième terme de l’équation de M axwell − F araday relatif à la variation temporelle de l’induction peut être négligé : −→rot −→E = − −→∂B ∂t ≈ 0 Dans un tel contexte, les éventuelles pertes par courant de F oucault au rotor sont négligeables. Cette approximation est légitime pour les machines basse vitesse.
Bobinages polyphasés considérés
Le bobinage d’une machine polyphasée se con¸coit comme l’extrapolation d’un bobinage triphasé. Les conditions d’obtention d’équilibre sont donc les mêmes qu’en triphasé. Aussi, la nature régulière ou irrégulière du bobinage se définit de la même manière. Et, quelque soit le nombre de phase, un bobinage équilibré doit répondre à des critères de périodicité et d’équivalence de phase bien précis. Tous ces aspects sont abordés dans les quatre paragraphes suivants.
Principe d’obtention
d’un bobinage équilibré Les références sur les techniques de bobinage concernent surtout les structures triphasées. L’ouvrage [8] étudie de manière exhaustive les techniques de bobinage des machines triphasées et la référence [17] donne les éléments pour la généralisation à un nombre quelconque de phases. L’analyse de l’ensemble bibliographique permet la synthèse suivante : le bobinage d’une machine polyphasée peut être vue comme la connexion de plusieurs bobines dont la répartition sur la circonférence de la machine doit être la plus régulière possible. En d’autres termes, l’ensemble des bobines constituant une phase doit générer des pôles Nord et Sud régulièrement espacés lorsque la phase est alimentée par un courant constant. Le bobinage est alors équilibré. Cette notion d’équilibre est illustrée par la figure II.2. Les axes de phases représentés sur la figure II.2 symbolisent les axes des bobines constituant la phase : le nombre d’axes d’une phase donnée est donc égal au nombre de paires de pôles de la machine. Pour obtenir un bobinage polyphasé équilibré, il faut maintenir cette disposition régulière des axes de phases le long de la machine. Concrètement, en cas de non respect de cette condition, les forces électromotrices de phase ne constituent plus un système régulièrement décalé en 2π Nω et la matrice d’inductance n’est plus circulante. En conséquence, la décomposition multimachine n’est plus utilisable.