Cours Gratuit
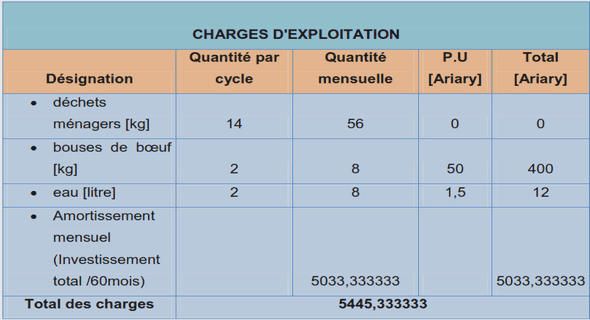
Polynomes polaires associés aux polynoms lp
Espaces Hp ( )
Contour de Jordan rectifiable
Définition 4.1.1. On appelle contour de Jordan, líimage díune application z : t ! z (t) définie de [a; b] ! C continue et telle que z (a) = z (b) et z j[a;b]est une application injective. Définition 4.1.2Un contour de Jordan est dit rectifiable si líapplication z est à variation bornée, dans ce cas sa variation totale notée V (z) est égale à la longueur du contour et coincide exactement avec R b a jz 0 (t)j dt < +1 lorsque z est dérivable.
Transformation conforme
La transformation conforme représente líun des outils fonctionnels fondamentale dans cette étude, elle permettra le passage de líextérieur du contour vers líextérieur du cercle G: Il est connu que tout contour de Jordan E partage le plan C en deux parties, líune bornée, L ouverte et simplement connexe appelée líintérieur de E et notée int(E) et líautre ouverte, non bornée et connexe appelée líextérieur de E notée Ext(E): Notons par = Ext(E) [ f1g et par G = fw 2 C : jwj > 1g [ f1g : Líapplication du théorème de la représentation conforme de Riemann [56],[61] ,[63]nous donne le théoréme suivant : Théorème 4.1.1 .Soit E un contour de Jordan du plan complexe C , alors il existe une application unique ‘ appelée transformation conforme, ‘ : ! G qui applique conformément líextérieur du contour vers líextérieur du disque possèdant les propriétés suivantes : (i) ‘ est bijective. (ii) ‘ j nf1gest holomorphe. (iii) ‘ (1) = 1: (vi) limz!1 ‘ (z) z = > 0: On note par C .
Télécharger le document complet
