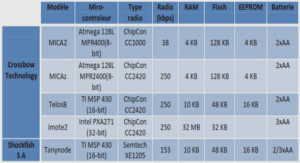
Contributions à l’étude d’espaces de fonctions et d’EDP dans une classe de domaines à frontière fractale auto-similaire

Contributions à l’étude d’espaces de fonctions et d’EDP dans une classe de domaines à frontière fractale auto-similaire

The Hausdorff dimension of Γ ∞

Recall that the open set condition is satisfied by the similitudes f 1 and f 2 if and only if there is a nonempty bounded open subset ω of R 2 such that f 1 (ω)∩ f 2 (ω) = ; and f 1 (ω)∪ f 2 (ω) ⊂ ω. In this case, the Hausdorff dimension of the invariant set Ξ is given by the single number d > 0 satisfying 2a d = 1 ( see §1.1.2, see also [Mor46, Kig01]). For a given θ ∈ (0,π/2), let (α,β) satisfy Assumption 1. For 0 < a ¶ a ⋆ , the open set condition is satisfied with ω = Ω because 2.2 The Geometry 65 ⋄ f 1 (Ω) ∩ f 2 (Ω) = ;, which stems from point (ii) in Assumption 1 if a < a ⋆ , and from Remark 2.2.2 if a = a ⋆ ; ⋄ by construction of Ω, we also have f 1 (Ω) ∪ f 2 (Ω) ⊂ Ω. Therefore, the Hausdorff dimension of the set Γ ∞ is d := dimH (Γ ∞) = −log2/ loga, If 0 < θ < π/2, then 0 < a ¶ a ⋆ < 1/ p 2 and d < 2. We have seen in paragraph 2.2.1.b that in the case when θ ∈ π 2N , the set Ξ is not countable. It is easy to compute its Hausdorff dimension in this case. Proposition 2.2.1 – If θ ∈ π 2N , then the Hausdorff dimension of Ξ is d/2. Proof. Take x ∈ R 2 . We have seen that Ξ = { fσ (x), σ ∈ 12m+1 (12|21) ∞}, where θ = π 2m . Therefore, Ξ = f 12m+1 ({ fσ (x), σ ∈ (12|21) ∞}). The set { fσ (x), σ ∈ (12|21) ∞} is exactly the invariant set of the contracting similitudes f 1 ◦ f 2 and f 2 ◦ f 1 , which also satisfy the open set condition with the domain Ω. Since their ratio is a 2 , we deduce that the Hausdorff dimension of Ξ is d/2. 

The self-similar measure µ

To define traces on Γ ∞, we recall the classical result on self-similar measures, see [Fal97, Hut81] and [Kig01] page 26: Theorem 2.2.4 – There exists a unique Borel regular probability measure µ on Γ ∞ such that for any Borel set A⊂ Γ ∞, µ(A) = 1 2 µ € f −1 1 (A) Š + 1 2 µ € f −1 2 (A) Š . (2.31) The measure µ is called the self-similar measure associated to the self-similar triplet (Γ ∞, f 1 , f 2 ). Proposition 2.2.2 – The measure µ is a d-measure on Γ ∞, with d = −log2/ loga: there exists two positive constants c1 and c2 such that c1 r d ¶ µ(B(x,r)) ¶ c2 r d , for any r 0 < r < 1 and x ∈ Γ ∞, where B(x,r) is the Euclidean ball in Γ ∞ centered at x and with radius r. In other words the closed set Γ ∞ is a d-set (see §1.2.6.a and [JW84]). Proof. The proof stems from the Moran condition. It is due to Moran [Mor46] and has been extended by Kigami ( see [Kig01], Proposition 1.5.8 and Theorem 1.5.7). We define L p µ , p ∈ [1,+∞) as the space of the measurable functions v on Γ ∞ such that R Γ ∞ |v| p dµ < ∞, endowed with the norm kvkL p µ = €R Γ ∞ |v| p dµ Š1/ p . We also introduce L ∞ µ , the space of essentially bounded functions with respect to the measure µ. A Hilbertian basis of L 2 µ can be constructed with e.g. Haar wavelets. 

Additional notations

We define the sets Γ σ = fσ (Γ 0 ) and Γ N = ∪σ∈AN Γ σ . The one-dimensional Lebesgue measure of Γ σ for σ ∈ AN and of Γ N are |Γ σ | = a N |Γ 0 | and |Γ N | = (2a) N |Γ 0 |. We will sometimes use the notation ® or ¦ to indicate that there may arise constants in the estimates, which are independent of the index n in Γ n , or of the index σ in Γ σ or Γ ∞,σ . We may also write A≃ B if A ® B and B ® A. 2.3 Trace results in the ramified domains Hereafter, we consider a ramified domain Ω constructed as in Section 2.2 with θ in (0,π/2), and we suppose that the parameters α,β satisfy Assumption 1. We first discuss very briefly the less interesting case when a < 1/2. If a < 1/2, then d < 1 and Γ ∞ is totally disconnected, see [Fal86], Lemma 4.1 p.54. This implies that f 1 (Γ ∞) ∩ f 2 (Γ ∞) = ;, see [Kig01], Theorem 1.6.2 page 33. The results of Jones[Jon81] and of Jonsson and Wallin [JW84] can be combined to prove that if p > max(1,2 − d), then the space of the traces on Γ ∞ of the functions v ∈ W 1, p (Ω) is B p, p 1− 2−d p (Γ ∞) ( see the introduction for the definition). We will see in Theorem 2.3.1 below that in this case, B p, p 1− 2−d p (Γ ∞) = JLip (1 − 2−d p , p, p;0;Γ ∞). Since the case a < 1/2 is understood, in the remaining part of the paper, we will take a such that 1/2 ¶ a ¶ a ⋆ , so the Hausdorff dimension d of Γ ∞ is not smaller than 1. We recall the construction of the trace operator made in [AT07] ( see also §1.3.3) by taking advantage of the self-simililarity; this trace operator, called ℓ ∞ below, is well defined even if a = a ⋆ . We first construct a sequence (ℓ n )n of approximations of the trace operator: consider the sequence of linear operators ℓ n : W 1, p (Ω) → L p µ , ℓ n (v) = X σ∈An ‚ 1 |Γ σ | Z Γ σ v d xŒ fσ (Γ ∞) , (2.32) where |Γ σ | is the one-dimensional Lebesgue measure of Γ σ . Proposition 2.3.1 – The sequence (ℓ n )n converges in L (W 1, p (Ω),L p µ ) to an operator that we call ℓ ∞. Proof. See [AT07]. Remark 2.3.1 – For a given θ, 0 < θ < π/2, let (α,β) satisfy Assumption 1 and Ω be constructed as in § 2.2.2.a, with 1/2 ¶ a ¶ a ⋆ ; in Chapter 4, we prove that Ω is a 2-set as defined in e.g. [JW84] page 205, i.e. there exist three positive constants r0 , c1 and c2 such that for any closed ball B(P,r), P ∈ Ω, 0 < r ¶ r0 , c1 r 2 ¶ m2 (B(P,r) ∩ Ω) ¶ c2 r 2 , where m2 is the Lebesgue measure in R 2 . Since Ω is a 2-set, there is a classical definition of a trace operator on ∂ Ω, see for instance [JW84] page 206. It is interesting to compare the operator ℓ ∞, whose construction is based on the self-similarity properties, with the latter classical trace operator. In Chapter 4, we prove that if p > 1, the two definitions of the trace of a function u ∈ W 1, p (Ω) coincide µ-almost everywhere. 

Trace results in the ramified domains 

Definition of JLip(t, p, p; 0;Γ ∞) for 0 < t < 1. The spaces JLip (t, p, p;0;K) on a self-similar set K were introduced in Definition 1.2.4. We recall here the definition of these spaces in the special case when K = Γ ∞. It was proved in [AT10] that this definition coincides with the original and more general one that was proposed in [Jon04]. Consider a real number t, 0 < t < 1. For any function f ∈ L p (Γ ∞), define |f | JLip(t, p, p;0;Γ ∞) by: |f | JLip(t, p, p;0;Γ ∞) =    X n¾0 2 n p t d 2 n( p 2 −1) X σ∈An |βσ | p    1 p , (2.33) where the numbers βσ , σ ∈ A are the coefficients of f in the Haar wavelet basis expansion given in (1.26). Definition 2.3.1 – A function f ∈ L p µ (Γ ∞) belongs to JLip (t, p, p;0;Γ ∞) if and only if the norm k f kJLip(t, p, p;0;Γ ∞) = |P0 f | + |f | JLip(t, p, p;0;Γ ∞) (2.34) is finite, where P0 f = R Γ ∞ f dµ. Recall that if the fractal set Γ ∞ is totally disconnected, then JLip(t, p, p;0;Γ ∞) coincides with the more classical function space: Theorem 2.3.1 – (Jonsson) If a < a ⋆ , then f 1 (Γ ∞) ∩ f 2 (Γ ∞) is empty and JLip (t, p, p;0;Γ ∞) = Lip(t, p, p;0;Γ ∞) = B p, p t (Γ ∞).

Characterization of the traces on Γ ∞ of the function in W 1, p (Ω)

Recall that the following theorem was proved in [AT10]. Theorem 2.3.2 – For a given θ, 0 < θ < π/2, let (α,β) satisfy Assumption 1 and Ω be constructed as in § 2.2.2.a, with 1/2 ¶ a ¶ a ⋆ ; then for all p, 1 < p < ∞, ℓ ∞ W 1, p (Ω)  = JLip (1 − 2−d p , p, p;0;Γ ∞). (2.35) First consequence A first consequence of Theorem 2.3.2 is that if 1/2 ¶ a < a ⋆ , then d ¾ 1 and from Theorem 2.3.1, ℓ ∞ W 1, p (Ω)  = Lip(1 − 2−d p , p, p;0;Γ ∞) = B p, p 1− 2−d p (Γ ∞), ∀p ∈ (1,+∞). (2.36) Remark 2.3.2 – Note that (2.36) has been proved in [AT08], without relying on the JLip spaces: indeed, when a < a ⋆ , Ω is an (ǫ,δ)-domain and Γ ∞ is a d-set; in this case, the extension result of Jones [Jon81] (from W 1, p (Ω) to W 1, p (R 2 )) and the trace result of Jonsson and Wallin [JW84] (from W 1, p (R 2 ) onto B p, p 1− 2−d p (Γ ∞)) can be combined to obtain (2.36).